Graph Shortest Path in Map-Reduce

Acknowledgements

I did not invent the concept behind this algorithm. I've seen it described in various places, for example here (among others). But none of them went into sufficient detail to write code that worked and was efficient. I recently had a few hours on a cross-country flight so I got out my pencil and worked this out.

Overview and Motivation

Dijkstra came up with the classic shortest path algorithm. It is efficient but inherently single threaded.

Suppose we have a BIG directed graph and we want to find the shortest path between any 2 nodes. One application of this might be LinkedIn: finding people who are 1st, 2nd, 3rd etc. contacts away from each other. Given 2 people in the social network graph, what is the shortest path connecting them? As of today - Feb 23 2012 - LinkedIn has about 150M members. That's a graph with 150M nodes and up to 150M squared = 22.5T (trillion) vertices. Of course it's quite sparse so the actual number of vertices is less, but even if it's 90% sparse that's still over 2T vertices!

Now suppose we want to compute the shortest path between any 2 nodes. Djikstra's algorithm would be efficient but being single threaded, would take a long time. It's difficult (impossible?) to parallelize, so we can't scale it horizontally across lots of hardware. Hardware is cheap. An algorithm that is less efficient but massively parallel could solve the problem much faster.

Consider a Map-Reduce job on a small-medium cluster of 100 machines, 8 cores each. That's 800 parallel threads. An algorithm half as efficient as Djikstra still runs 400 TIMES faster. That's the difference between solving the problem overnight, versus taking a year!

Algorithm: Setup

We start by expressing the graph in a form that plays well with Hadoop. Define "A" as the start node. Create a text file, each line describing a node. Nodes without children do not need to be listed.
Node ID, distance from A, color, list of child node IDs

KVP = Key Value Pair, for our purposes, a line of text describing a Node in the graph.

Color indicates the processing state of each node.

black: none - the node is straight from the original graph definition

grey: some - the node has been generated from analysis of a black node, but has not been fully processed

white: the node's children have been traversed/expanded

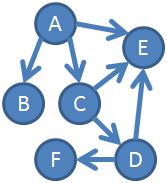
For example, this graph:

Is expressed as:
A, 0, black, B, C, E
C, ?, black, D, E
D, ?, black, E, F

LinkedIn's graph would be a file with 150M lines. At 500 bytes per line, that's 75M kilobytes or 75 GBytes. This is a big file, but easily manageable in HDFS. With the default HDFS block size of 64 MB, it's about 1200 blocks. That's 1200 mapper tasks, which nicely splits the load with a lot of parallelism. Smaller graphs might not have a file big enough to get enough mappers. In that case, a custom InputFormatter could be used to give each mapper a smaller chunk of data.

Algorithm: Goals

The algorithm needs to do 2 things:

Traverse the graph - expand child nodes.

Compute minimum distances - from node A to each node

In short, Mappers do the first and Reducers do the second. The longer more accurate story is that Mappers and Reducers do a little of both, but Mappers are primarily focused on the first and Reducers on the second.

Algorithm: Mapper

Mappers traverse the graph by expanding child nodes. For each input line:

The key is the node ID, value is the rest of the line (shown above).

If the line is white, emit it as-is with no changes

If the line is grey or black, change to "white" and expand its child nodes.

"Expand child nodes" means emit an additional line "grey" for the child, with distance = parent + 1

Algorithm: Reducer

Reducers combine distance & children into a single KVP.

The key is the node ID, value is the rest of the line

Distance is shortest of all appearing

Children are union of all appearing

If distance is known, child list is complete (tag empty to differentiate from unknown)

If distance is known and child list is empty, set color to white

Otherwise (if child list not empty), must remain grey so mapper will expand it

Key concept: Multiple mappers in the same pass may emit different values for the same key. For example, in the above graph E has 3 parents: A, C and D. One mapper may emit a record (KVP) for E by expanding node A, another emits a KVP for E by expanding C, another by expanding D. The reducer will get all these records and compute:

The children as the union of all children

The distance as the minimum of all distances

Algorithm: Summary

Mappers expand children.

Emit 1 KVP for each

Each child is Grey with distance = parent distance + 1 (or ? if parent distance is not known)

Once expanded, parent becomes white (even if distance not known)

How to detect when complete (further MR cycles not needed)

Reducers set job counter to number of KVP emitted for which distance is unknown

When 0, we're done

White means node has been expanded. It does not mean distance is known.
Theorem: for any given node, distance is known no earlier than children are expanded.

Algorithm: Details

The above graph would be processed in 3 MR passes as follows:

Startup:
A, 0, black, B, C, E
C, ?, black, D, E
D, ?, black, E, F

Pass 1

Map:

Input: A, 0, black, B, C, E
Emit:
A, 0, white, B, C, E
B, 1, grey, ?
C, 1, grey, ?
E, 1, grey, ?

Input: C, ?, black, D, E
Emit:
C, ?, white, D, E
D, ?, grey, ?
E, ?, grey, ?

Input: D, ?, black, E, F
Emit:
D, ?, white, E, F
E, ?, grey, ?
F, ?, grey, ?

Reduce:

Input: A { 0, white, B, C, E }
Emit: A, 0, white, B, C, E

Input: B { 1, grey, ? }
Emit: B, 1, grey, ?

Input: C { 1, grey, ? } { ?, white, D, E }
Emit: C, 1, grey, D, E [NOTE: would emit "white" if child list was empty]

Input: D { ?, grey, ? } { ?, white, E, F }
Emit: D, ?, grey, E, F [NOTE: would emit "white' if child list was empty]

Input: E { 1, grey, ? } { ?, grey, ? } { ?, grey, ? }
Emit: E, 1, white, nil [NOTE: mark "white" since there are no children. How do we know that? Distance is known, and since we know distance is known no earlier than children, there must be no children, so we can mark it white]

Job count = 1 - one emitted KVP has unknown distance

Pass 2

Map:

Input: A, 0, white, B, C, E
Emit:
A, 0, white, B, C, E

Input: B, 1, grey, ?
Emit:
B, 1, grey, ?

Input: C, 1, D, E, grey
Emit:
C, 1, white, D, E
D, 2, grey, ?
E, 2, grey, ?

Input: D, ?, grey, E, F
Emit:
D, ?, white, E, F
E, ?, grey, ?
F, ?, grey, ?

Input: E, 1, -, white
Emit:
E, 1, -, white

Reduce:

Input: A { 0, white, B, C, E }
Emit: A, 0, white, B, C, E

Input: B { 1, grey, ? }
Emit: B, 1, white, - [NOTE: set to "white" since there are no children. See above note how we know that.]

Input: C { 1, white, D, E }
Emit: C, 1, white, D, E

Input: D { ?, white, E, F } { 2, grey, ? }
Emit: D, 2, grey, E, F [NOTE: set to "grey" since child list is not empty]

Input: E { ?, grey, ? } { 1, white, - } { 2, grey, ? }
Emit: E, 1, white, - [NOTE: set to "white" since child list is empty]

Input: F { ?, grey, ? }
Emit: F, ?, grey, ?

Job count = 1 - one emitted KVP has unknown distance

Pass 3

Map:

Input: A, 0, white, B, C, E
Emit:
A, 0, white, B, C, E

Input: B, 1, white, -
Emit:
B, 1, white, -

Input: C, 1, white, D, E
Emit:
C, 1, white, D, E

Input: D, 2, grey, E, F
Emit:
D, 2, white, E, F
E, 3, grey, ?
F, 3, grey, ?

Input: E, 1, white, -
Emit:
E, 1, white, -

Input: F, ?, grey, ?
Emit:
F, ?, grey, ?

Reduce:

Input: A { 0, white, B, C, E }
Emit: A, 0, white, B, C, E

Input: B { 1, white, - }
Emit: B, 1, white, -

Input: C { 1, white, D, E }
Emit: C, 1, white, D, E

Input: D { 2, white, E, F }
Emit: D, 2, white, E, F

Input: E { 3, grey, ? } { 1, white, - }
Emit: E, 1, white, - [NOTE: set to "white" since child list is empty.]

Input: F { 3, grey, ? } { ?, grey, ? }
Emit: F, 3, white, - [NOTE: set to "white" since child list is empty. See above note for why we know child list is empty.]

Job count = 0 - all distances in reducer emitted KVP are known.

DONE! We have computed the shortest path from A to every other node in the graph.
Result: A=0, B=1, C=1, D=2, E=1, F=3.
Check these distances against the above graph.