The Corda Soul uses the WM8741 DAC chip. Actually, it uses 2 of them, each in mono mode which gives slightly better performance. This chip has 5 different anti-aliasing reconstruction filters. The Corda Soul has a switch to select either of 2 different filters. Here I describe these filters, show some measurements I made, and from this make an educated guess which 2 of these filters the Corda Soul uses, at various sampling rates. At higher sampling frequencies the digital filter should make less difference; more on that here. My measurements and observations below are consistent with that.
Note: this DAC chip has a mode called OSR for oversampling. The Soul uses this chip in OSR high, which means it always oversamples the digital signal at the highest rate possible, to 192 or 176.4 kHz, whichever is an integer multiple of the source. For example, 44.1k is oversampled 4x to 176.4k and 96k is oversampled 2x to 192k. The function of the digital filters depends on this OSR mode.
Summary: the filters have 3 key attributes:
- Frequency Response: how fast (sharp) or slow they attenuate high frequencies.
- Frequency Response: the filter stop-band – is it above, at, or below Nyquist.
- Phase: whether the filter is linear (constant group delay, FIR) or minimum phase (variable group delay, IIR).
This table summarizes key filter attributes – taken from the WM8741 data sheet linked above, for 44.1k / 48k sampling in OSR high mode.
| Name | Rate | Phase | Passband | Stopband | Nyquist | Group Delay |
| 1 | sharp | lin [min?] | 20,021 / 21,792 | 24,079 / 26,208 | -6.02 | 43 |
| 2 | slow | min [lin?] | 17,993 / 19,584 | 23,020 / 25,056 | -28.07 | 8 |
| 3 | sharp | lin | 20,021 / 21,792 | 24,079 / 26,208 | -6.43 | 7 |
| 4 | slow | min | 18,390 / 20,016 | 22,050 / 24,000 | -116.19 | 47 |
| 5 | slow | lin | 18,390 / 20,016 | 22,050 / 24,000 | -122.6 | 8 |
Note: at 44.1 kHz sampling, filters 1 and 3 are almost identical. The first is called “soft knee” while the third is called “brickwall”. Yet strangely, their frequency response is the same (despite their names which suggest otherwise) and the only difference is that 1 has more group delay. This suggests that the labels for filters 1 and 2 might have been mistakenly reversed in the WM8741 data sheet. Brickwall is usually the standard sharp filter closest to the ideal mathematical response. But not here, because being only -6 dB at Nyquist, it can allow ultrasonic noise to leak into the passband.
Filters 4 and 5 are labeled as apodizing. From what I read, this means their stop-band is a little below Nyquist. Why set the stop-band below Nyquist? Theoretically this is unnecessary. The reason given is that rejecting the upper band just below Nyquist is supposed to be an extra-safe way of avoiding any distortion introduced by the AD conversion during recording. Here, the stop-band of the apodizing filters is at Nyquist, but that’s still a bit lower than the others which are above Nyquist (which is an improper implementation).
Based on the above chart, filter 5 is the most correct implementation because it is the only filter that is fully attenuated by Nyquist, with flat phase response (minimal group delay). However, filter 5 rolls off a little early to achieve this. If you want flat response to 20 kHz, filter 3 is the best choice, though it does so at the price of allowing some noise above Nyquist. If one wanted a minimum phase alternative, the best choice would be filter 4. Both 1 and 4 are minimum phase, but 1 is not fully attenuated at Nyquist. Filter 4 is. However, to achieve this, filter 4 sacrifices FR with an earlier roll off.
For comparison, here’s how these filters behave at 96k / 88.2 k sampling (also in OSR high mode).
| Name | Rate | Phase | Passband | Stopband | Nyquist | Group Delay |
| 1 | sharp | lin [min] | 19,968/18,346 | 48,000/44,100 | -120.41 | 17 |
| 2 | slow | min [lin] | 19,968/18,346 | 48,000/44,100 | –120.8 | 9 |
| 3 | sharp | lin | 40,032/36,779 | 48,000/44,100 | -116.89 | 48 |
| 4 | slow | min | 19,968/18,346 | 43,968/40,396 | -126.82 | 9 |
| 5 | slow | lin | 19,968/18,346 | 43,968/40,396 | -130.52 | 8 |
At these higher sampling rates, all the filters are fully attenuated by Nyquist (or lower). That’s a good thing and Wolfson should have done this at the lower rates too. Also, filters 1, 2, 4 and 5 (all but 3) take advantage of the higher sampling frequency to have a wide transition band with gentler slope. This sacrifices response above 20k (which we don’t need) to minimize passband distortion, particularly phase shift. The numbers reflect this, as they all have flatter (better) phase response than filter 3.
As with the first table, filters 1 and 2 look like a mis-print; both have the same transition and stop bands. But all else equal, linear phase should have less phase shift, not more. This is probably a typo, because as you’ll see below, the impulse response for filter 1 is asymmetric, and for filter 2 is symmetric, and symmetric impulse response usually implies linear phase.
Based on this data, filters 2, 3 or 5 are the most correct implementations. Filter 3 has flat FR up to 40 kHz, but this extra octave comes at the price of a narrower transition band having more phase shift and group delay. Filters 2 and 5 have flatter phase response but start rolling off around 20 kHz to get a wider transition band. If one wanted a minimum phase alternative, filters 1 or 4 are the only choices and either would be fine.
I measured the Soul’s output with the digital filter switch in each mode, sharp and slow, using 2 test signals: a frequency sweep and a square wave. From this, I measured frequency and phase response, group delay and impulse response. Charts/graphs are below, in the appendix.
Here’s the square wave: first sharp, then slow:
Overall, at 44.1 kHz I observed 3 key differences:
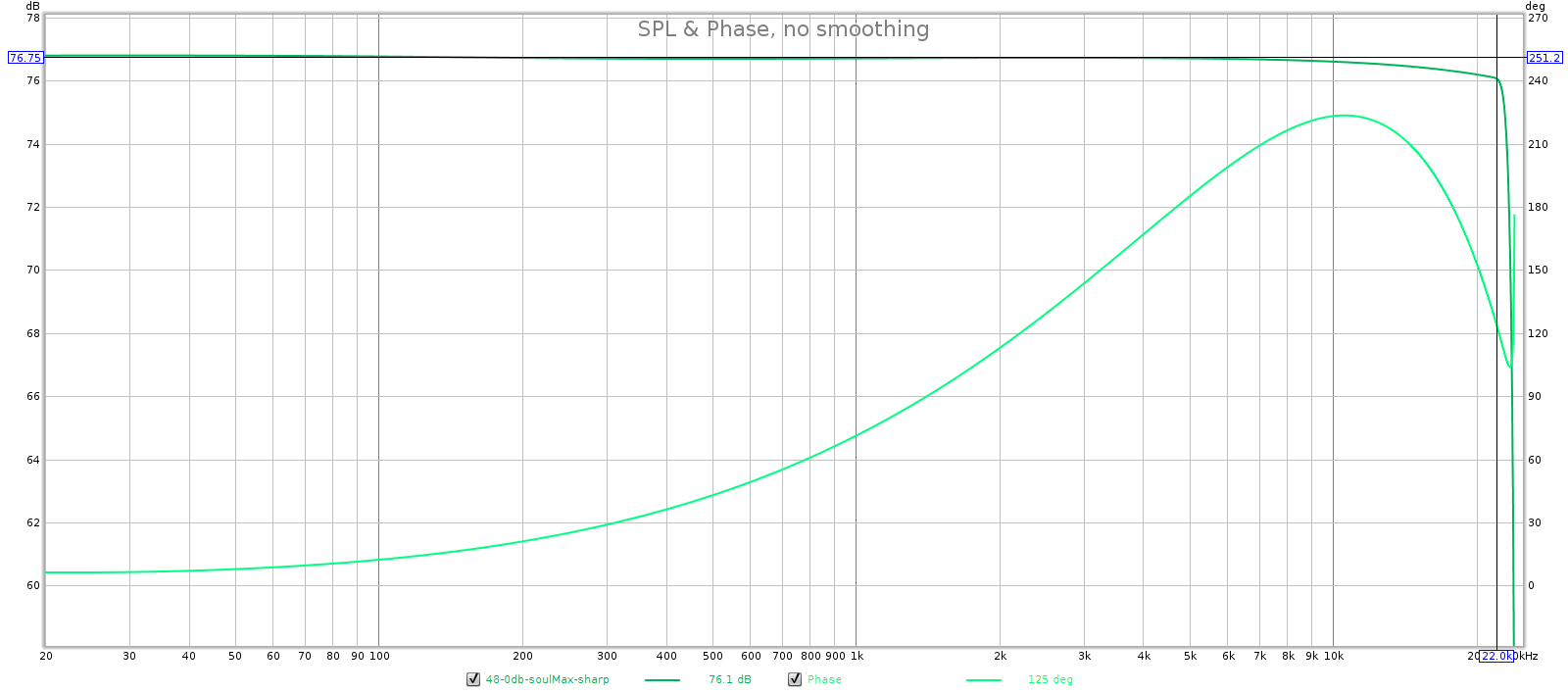
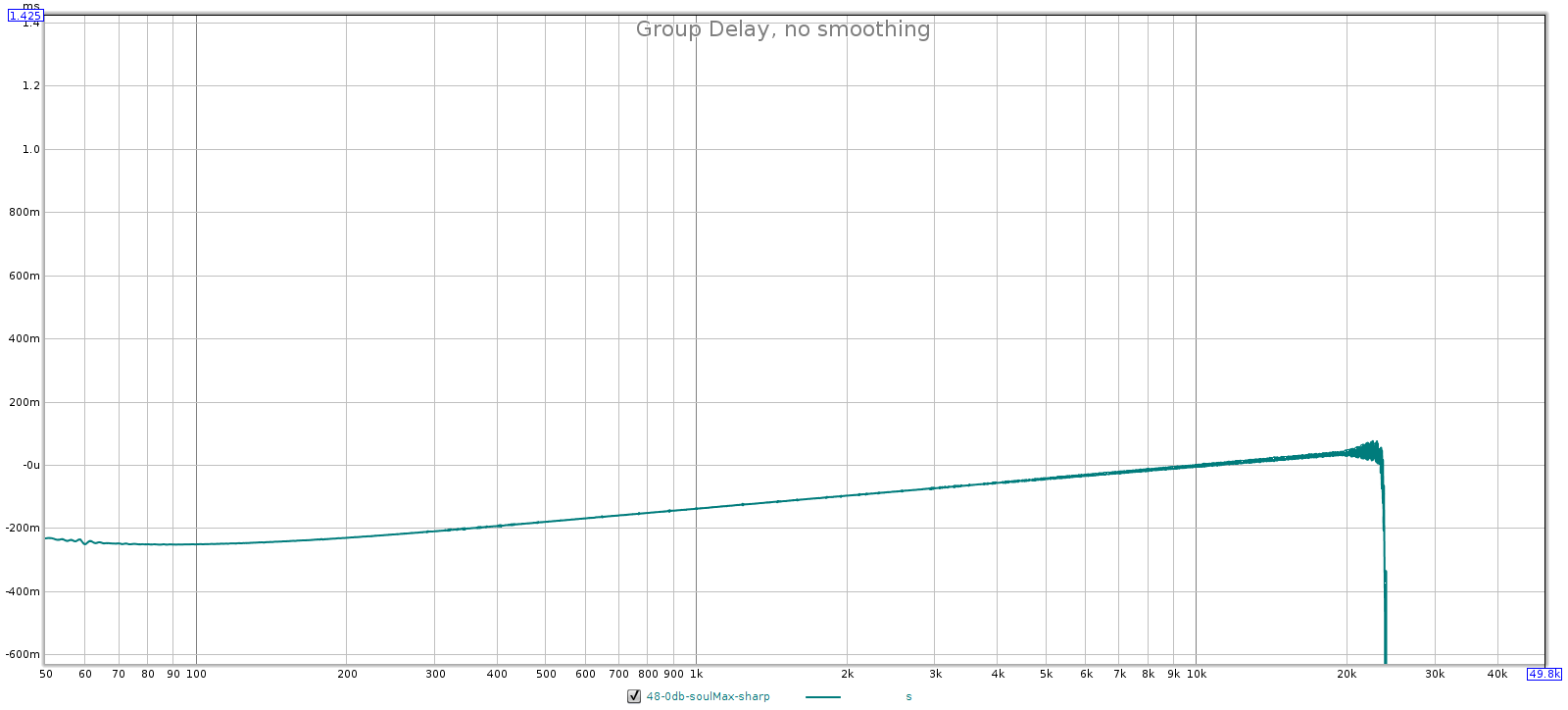
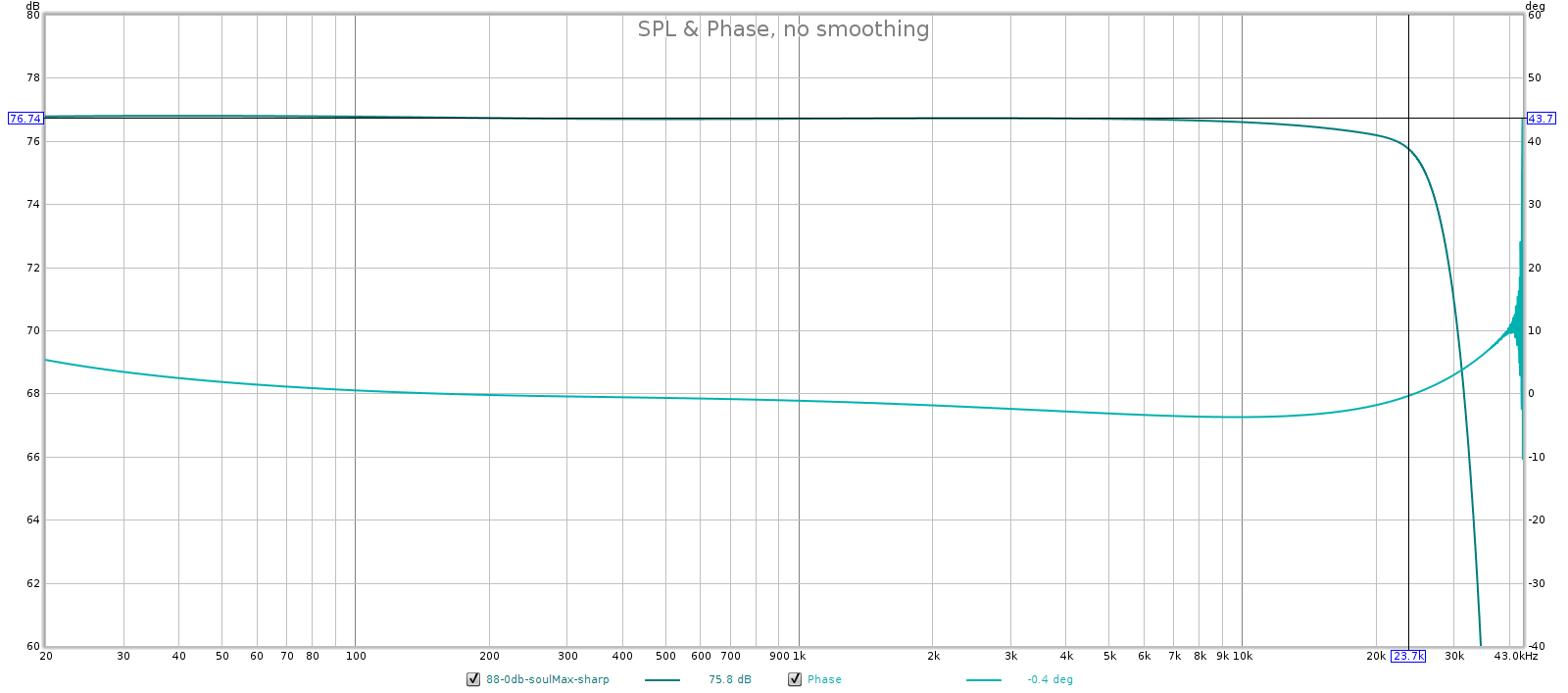
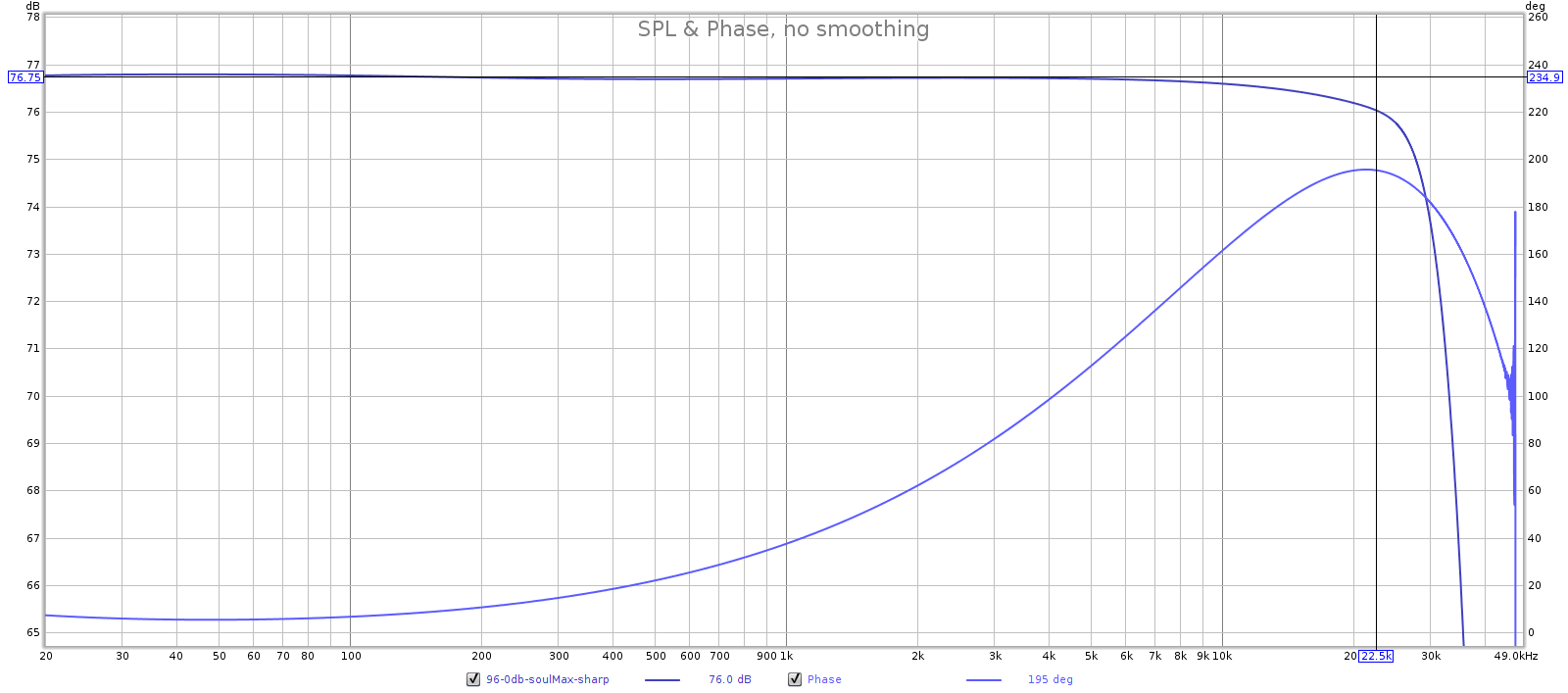
- In sharp mode, frequency response and group delay are both flat to 20 kHz.
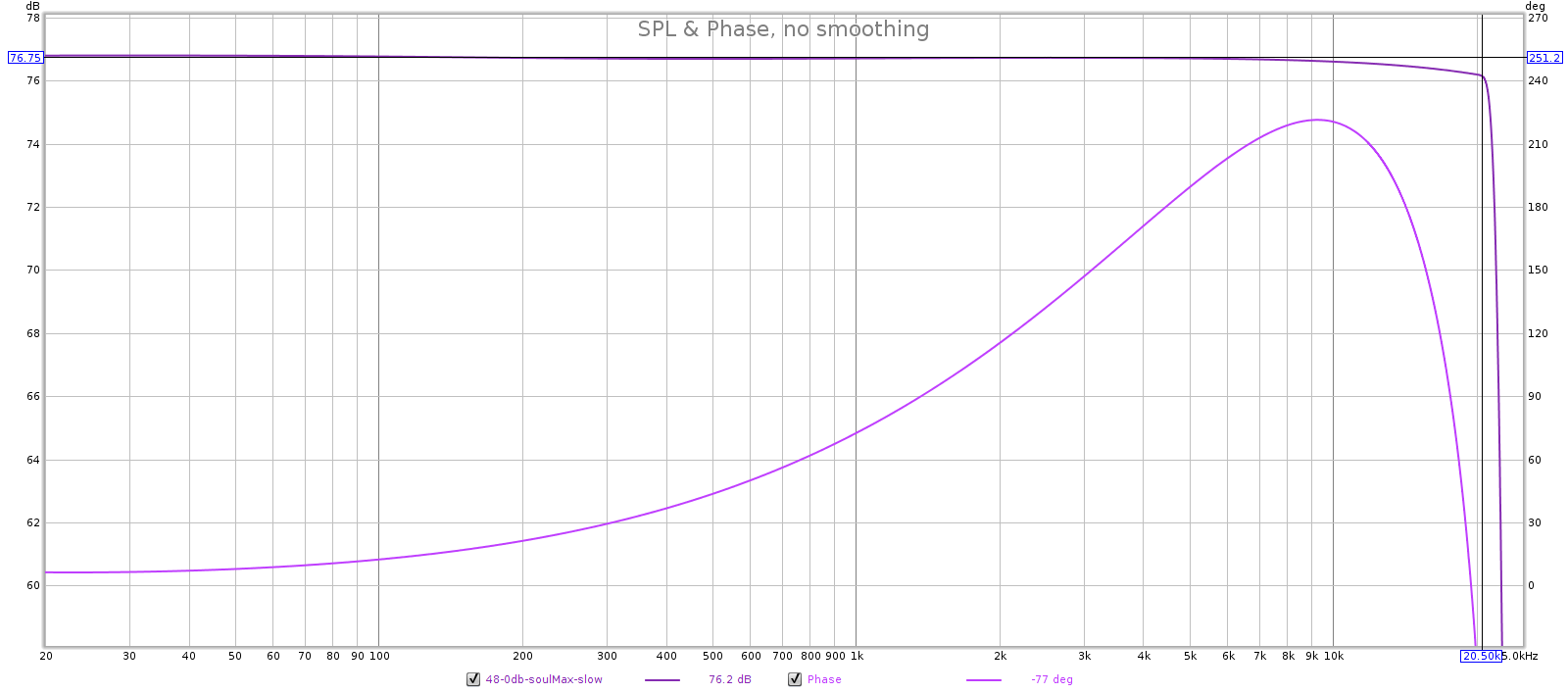
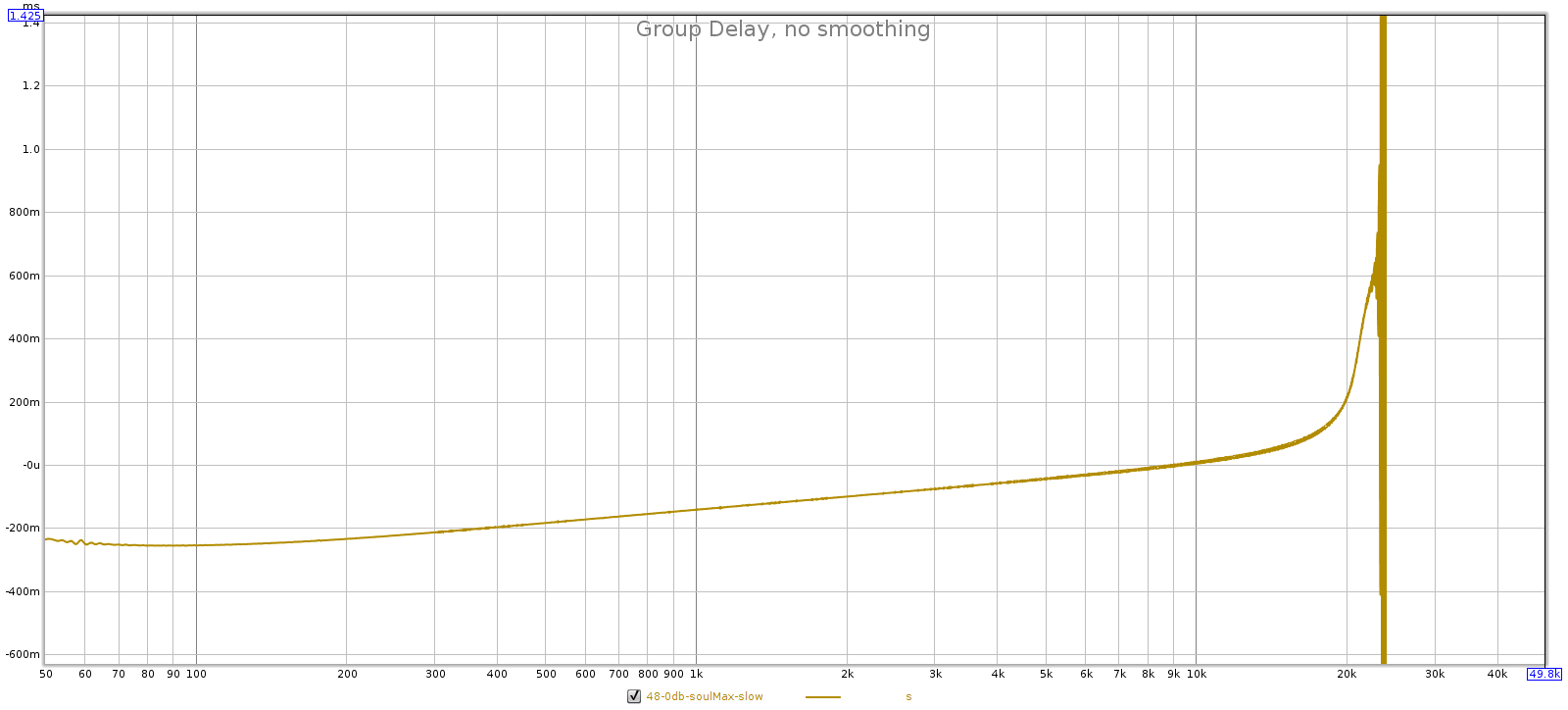
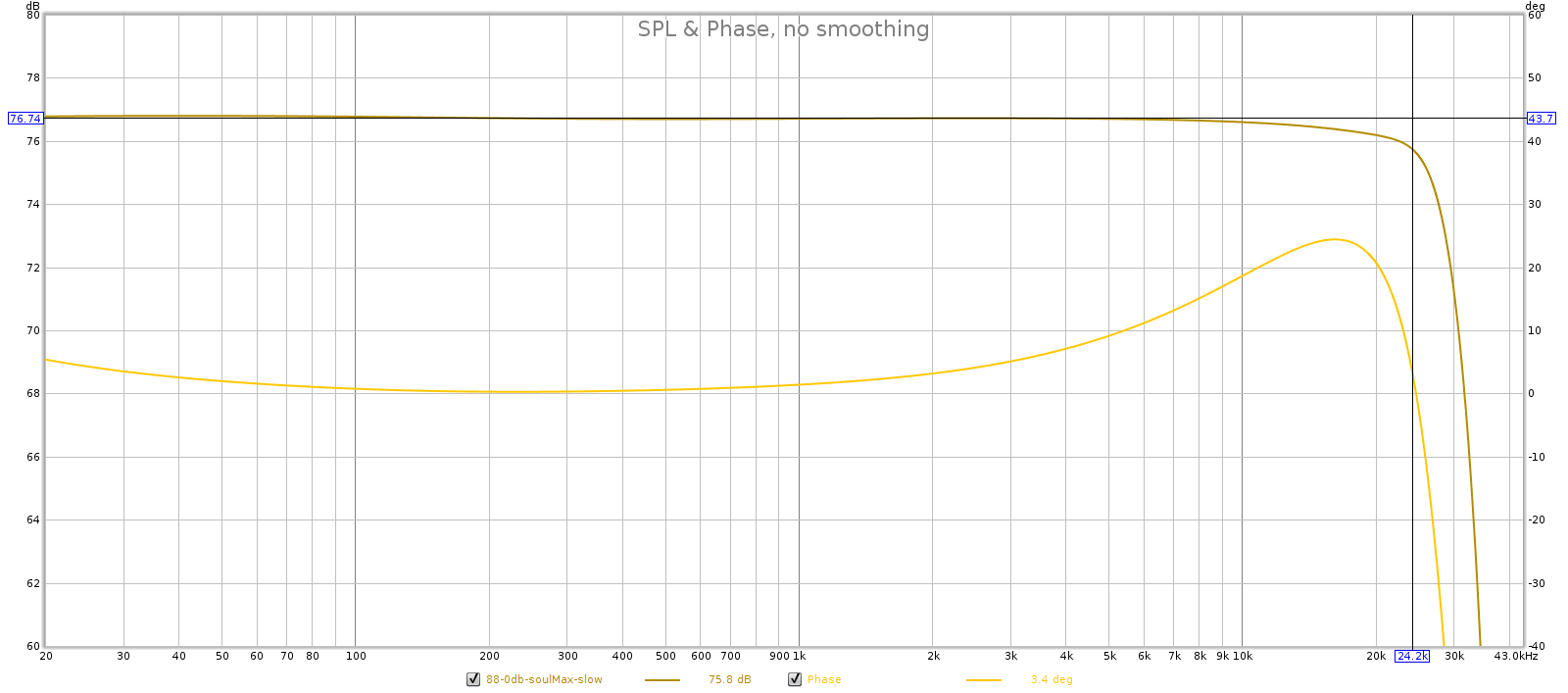
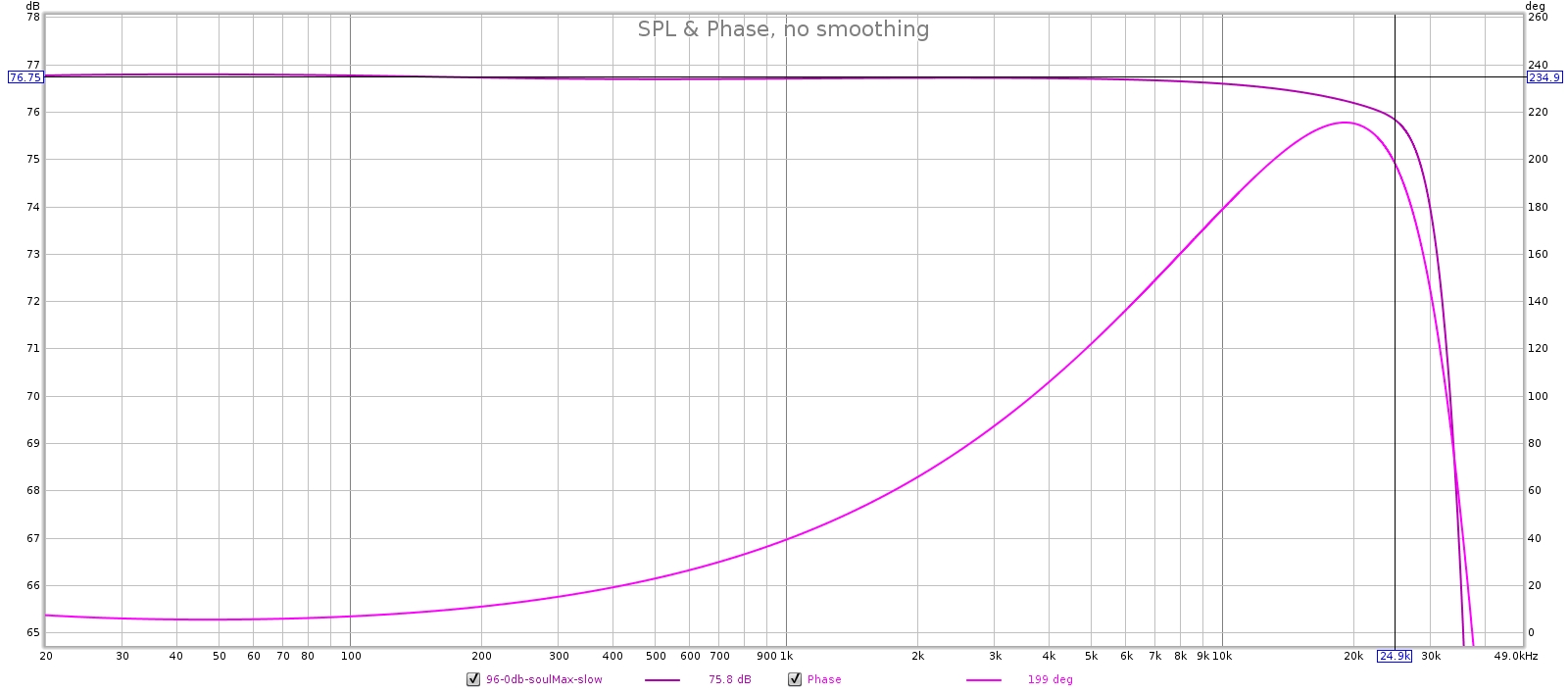
- In slow mode, frequency response starts to roll off and group delay starts to rise between 18 and 19 kHz.
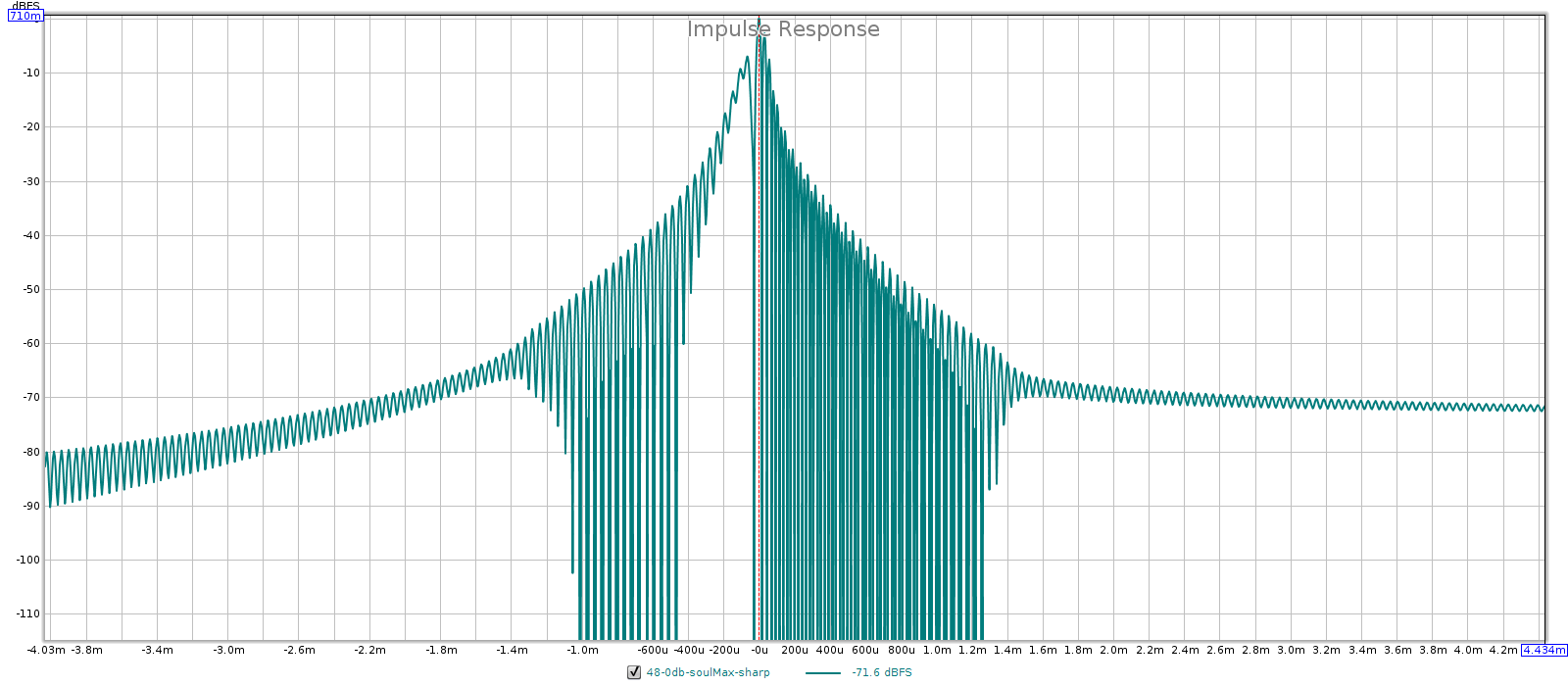
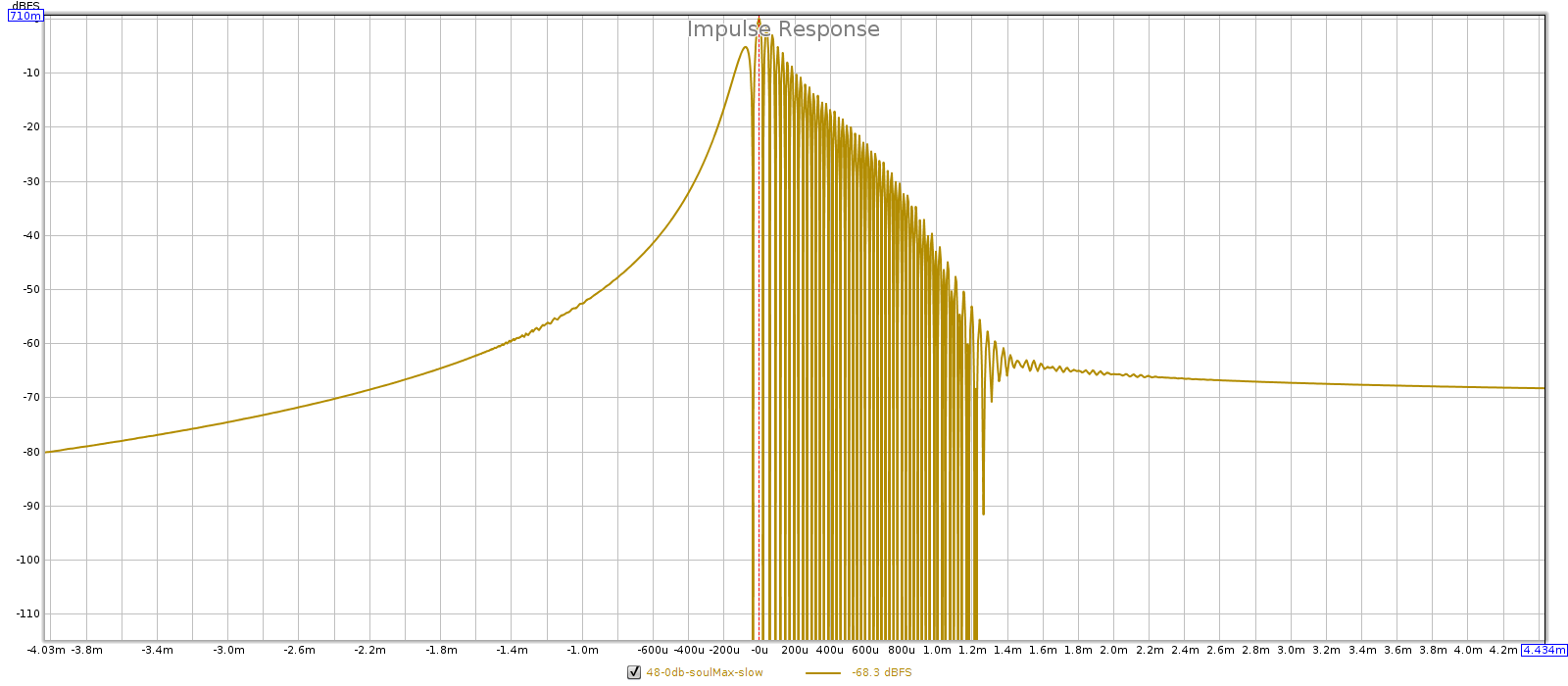
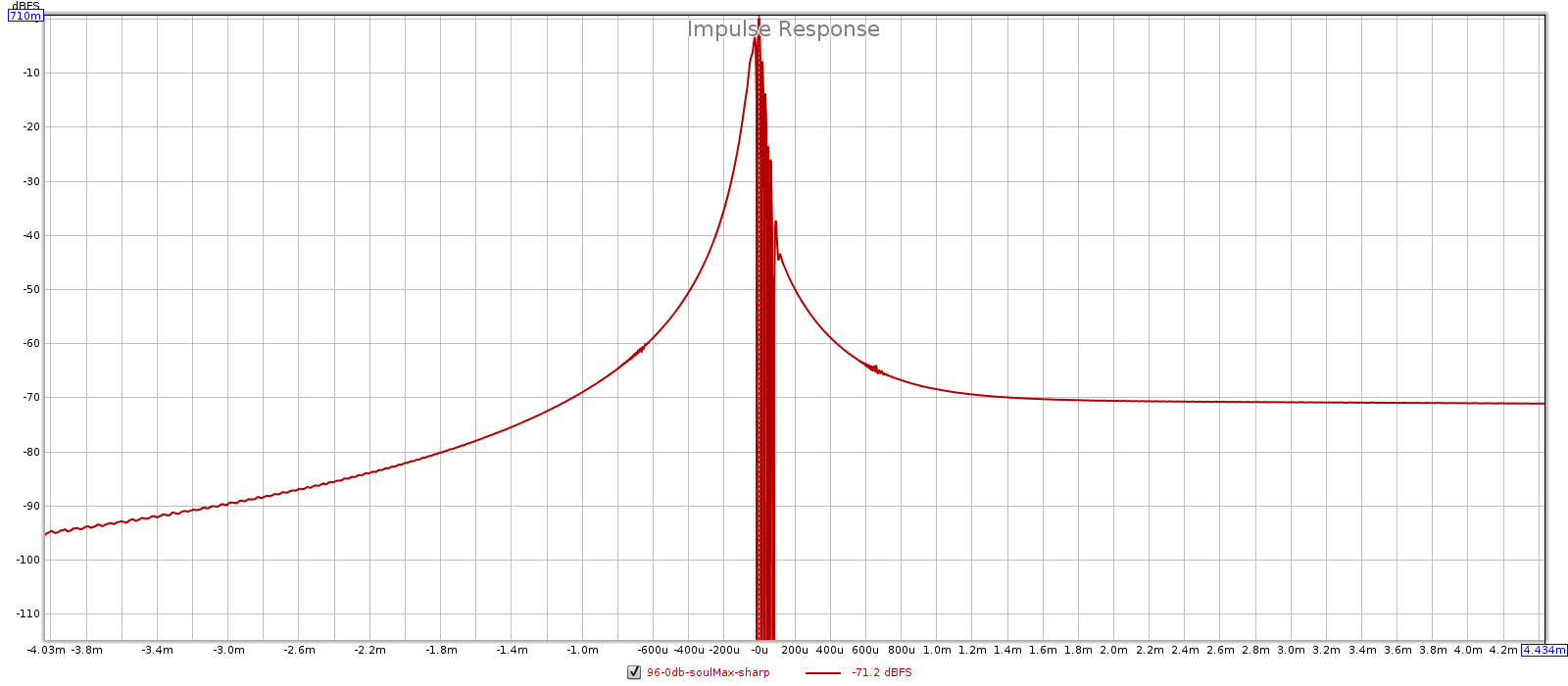
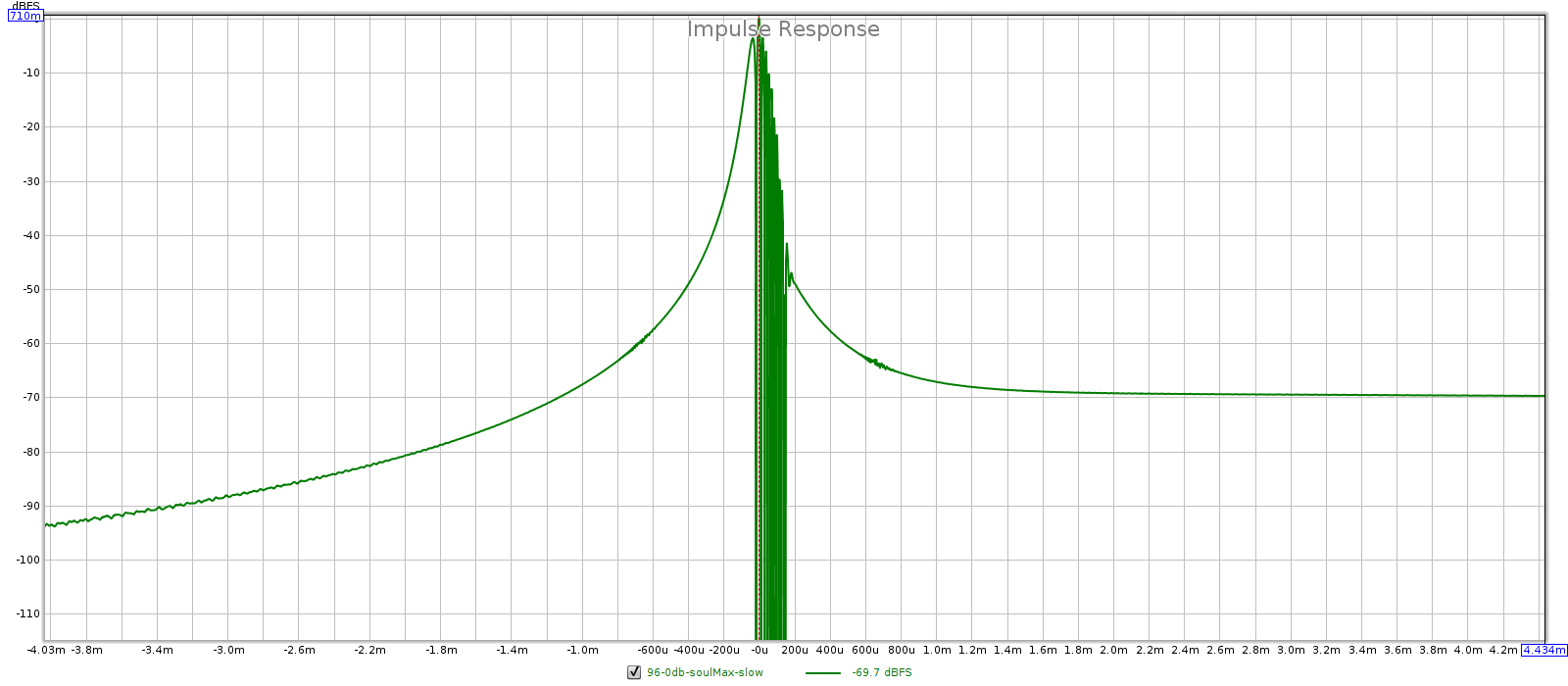
- In slow mode, the square wave shows no ripple before a transition, and ripples with greater amplitude and longer duration after a transition.
- The above curves are similar when comparing the sharp & slow filters at 48k sampling.
From these observations I conclude that for 44.1k and 48k signals, the Soul uses filters 3 and 4 in sharp and slow modes, respectively. Here’s why:
- Because FR is flat to 20 kHz in sharp mode, it must be using filter 1 or 3.
- Because GD is flat in sharp mode, it must be using filter 3.
- Because FR rolls off just above 18k in slow mode, it must be using filter 2, 4 or 5.
- Because GD rises in slow mode, it must be using filter 4.
Appendix
I recorded these graphs using my sound card, an ESI Juli@. This is not a great setup, but it’s the best I can do without dedicated equipment.
PC USB Audio output –> Corda Soul USB input –> Corda Soul analog output –> sound card analog input
Details:
- Configured the sound card for analog balanced input & output (flip its daughter board from unbalanced to balanced.
- Cabled from Soul to Juli@, using 3-pin XLR to 1/4″ TRS.
- On PC:
- Disable pulseaudio
- Use Room EQ Wizard (REQW) on PC, in ALSA mode
- Configure REQW
- set desired sampling rate (44.1, 48, 88.1, 96)
- set audio output to USB
- set audio input to Juli@ analog
- Configure Corda Soul
- Select USB audio input
- Ensure all DSP disabled (knobs at 12:00)
- Set volume as desired
- measured at max: 0 dB
- measured at 12:00; -16 dB; 34 clicks down
- Use REQW “Measure” function
- Confirm proper sampling rate light on Corda Soul
Important Note: My measurements depend as much on the Corda Soul as they do on the Juli@ sound card. For example, if the Juli@ rolls off the frequency response faster than the Soul, then I will measure the same FR in both mods of the Soul. And if the Juli@ applies a minimum phase filter that adds phase distortion, then I will measure that phase distortion in both modes of the Soul. This probably explains why the digital filter responses were so similar at 88 and 96 kHz.
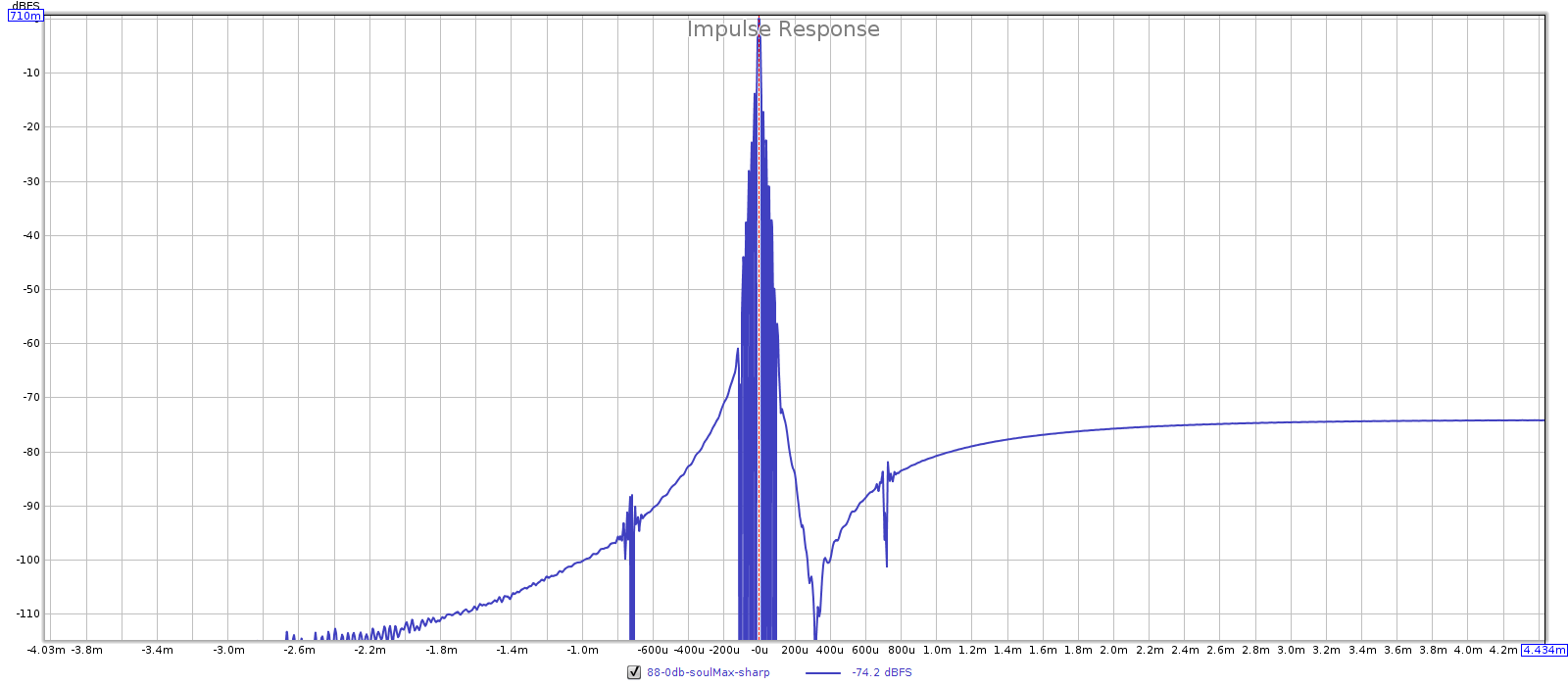
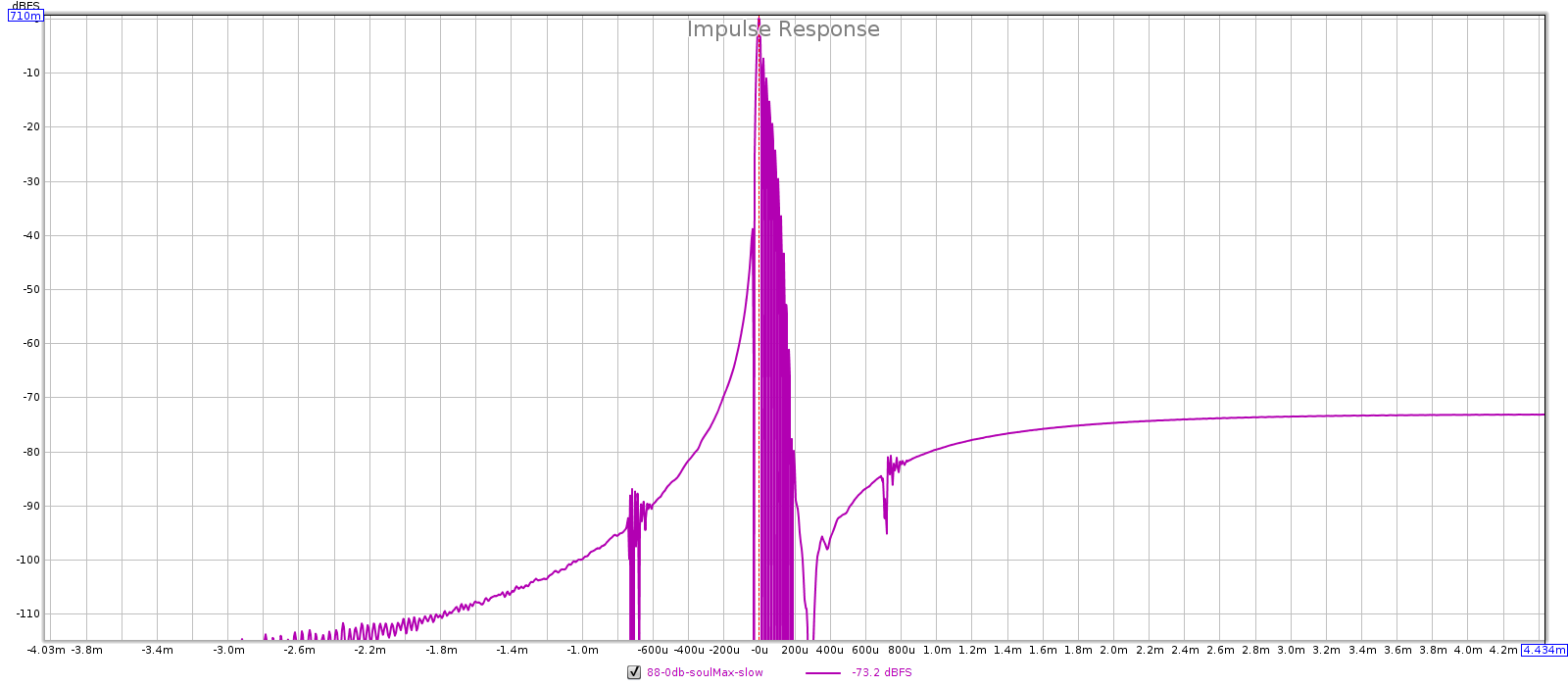
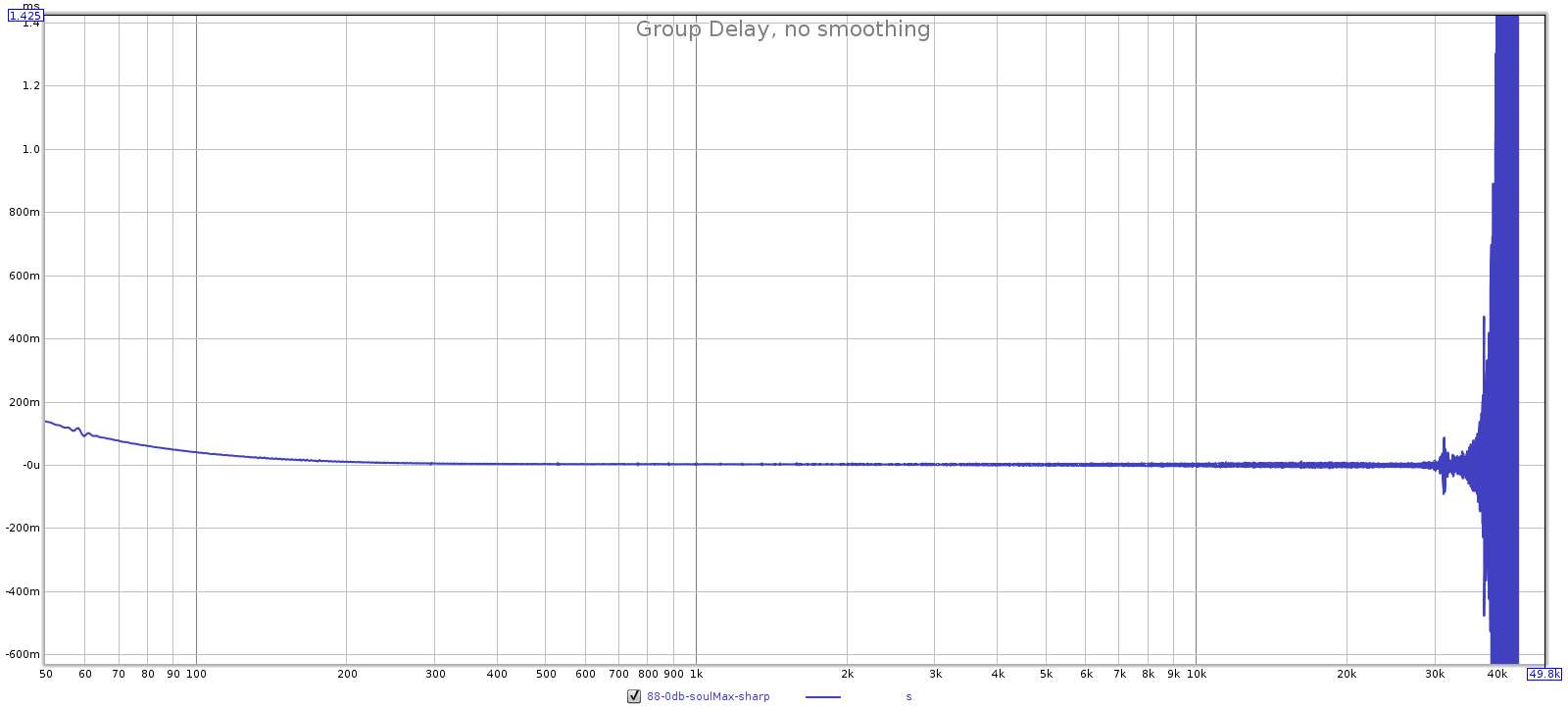
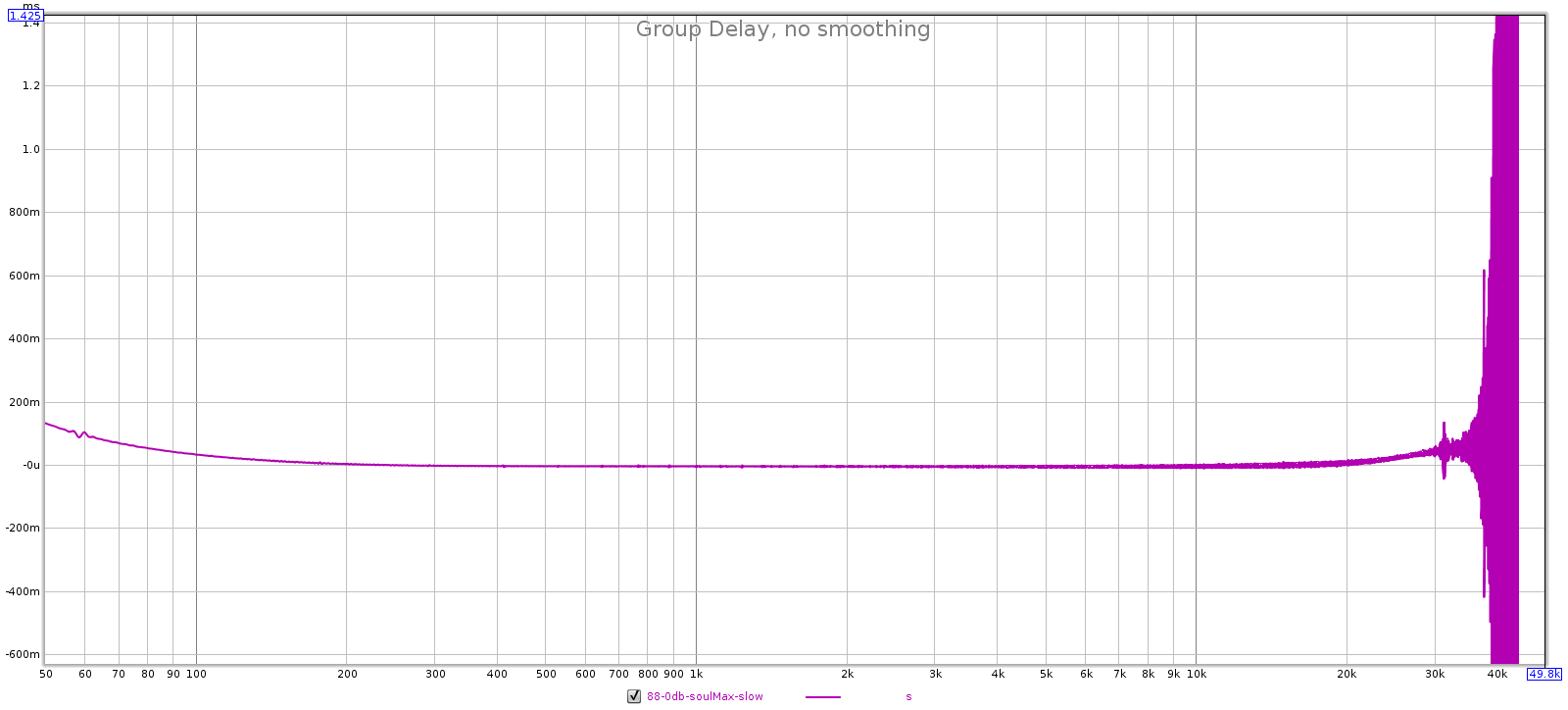
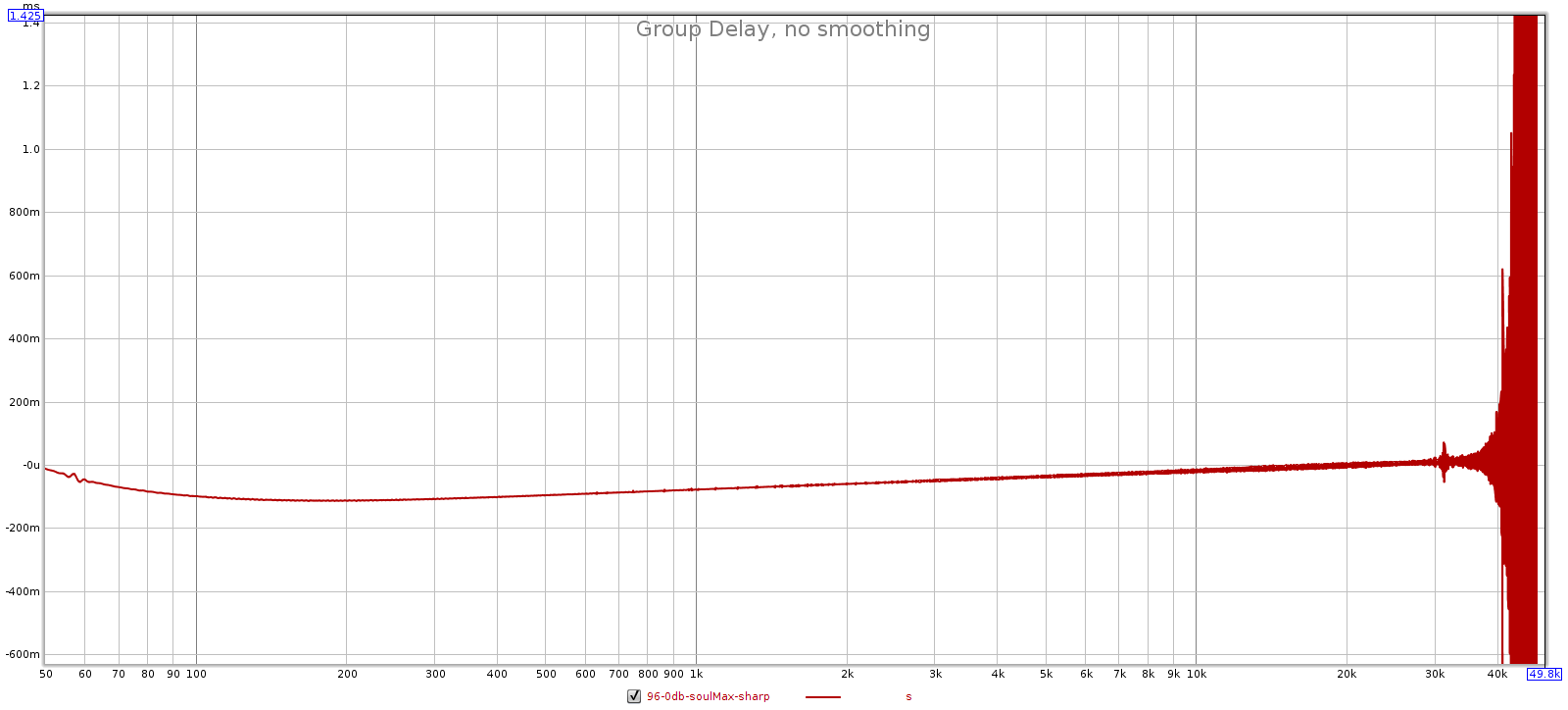
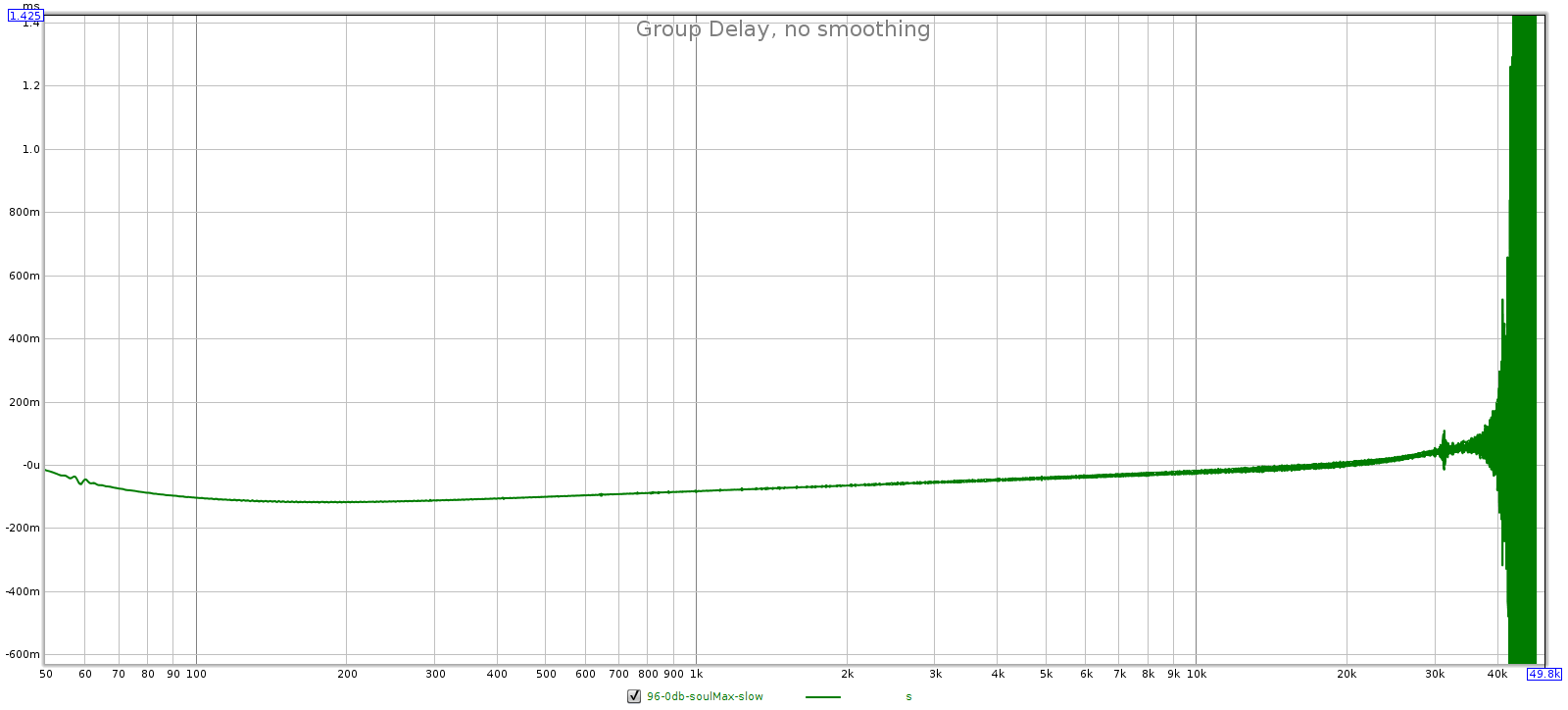
Here are FR, phase, GD and impulse plots for all tested sampling rates. Each is sharp top, slow bottom. Observe that at multiples of 44.1k (44.1k and 88.2k), the sharp filter has flat phase response while the slow filter does not. But at multiples of 48k (48k and 96k), both filters have similar non-flat phase response. This is probably due to the Juli@ card. However, the comments below assume the Juli@ card is transparent and all differences are due to the Soul.
In all cases, both filters at all sampling rates:
- Frequency response: starts to taper at 20 kHz for the widest possible transition band.
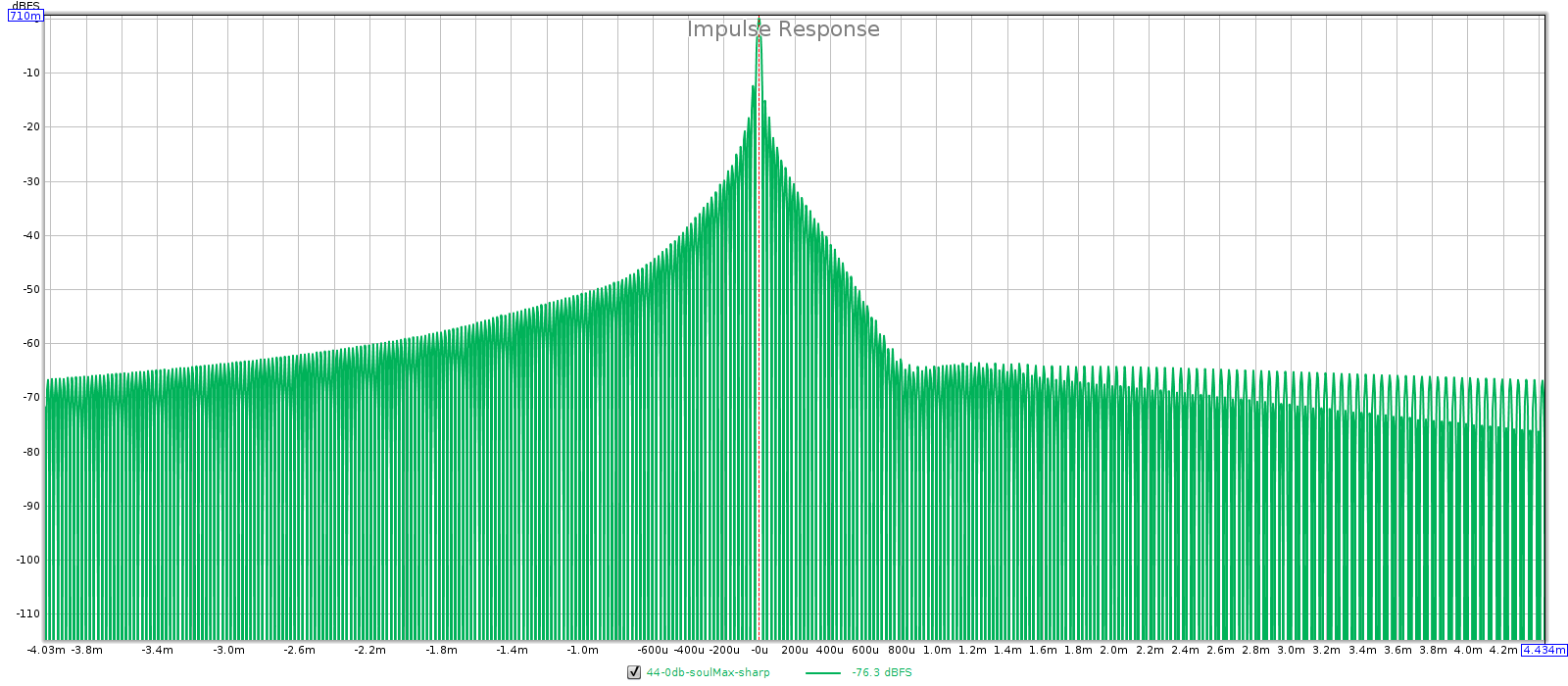
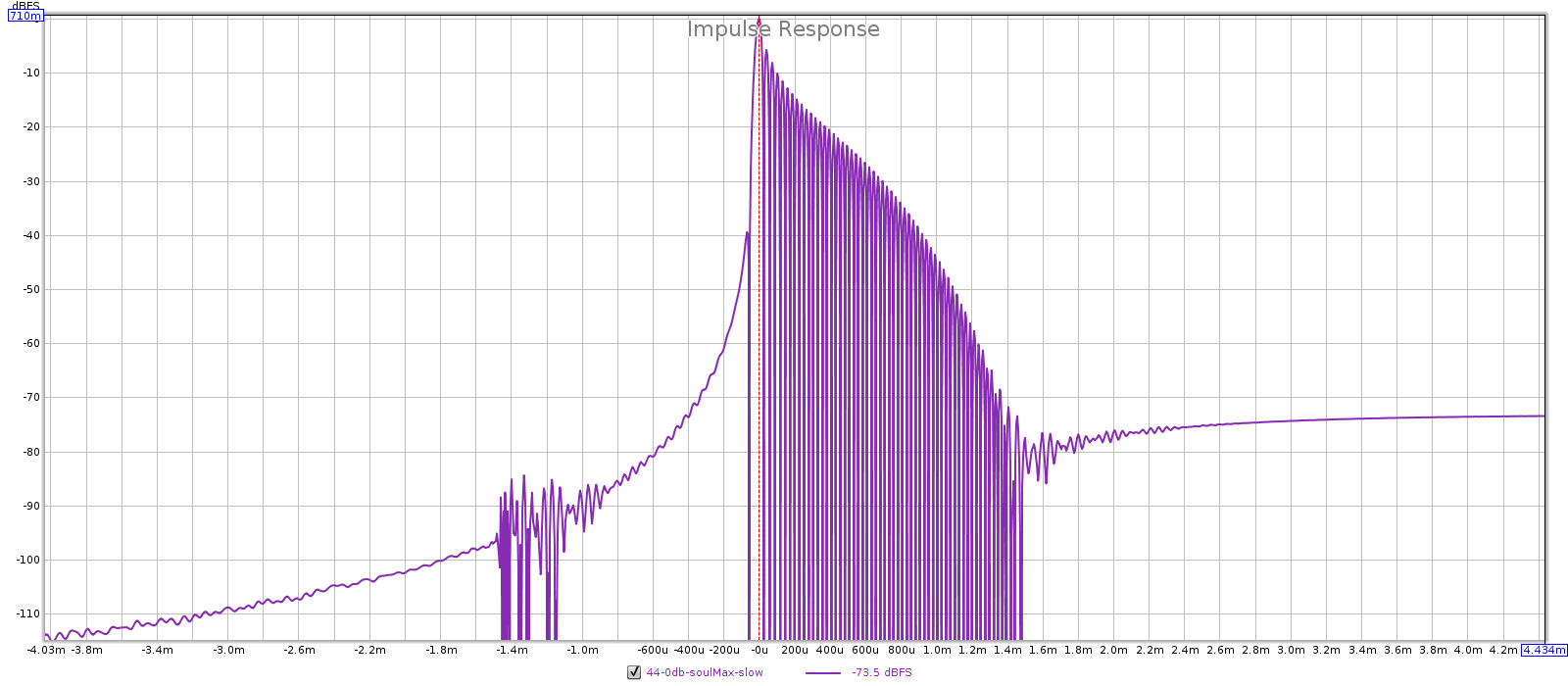
- Impulse response: sharp is symmetric, slow is asymmetric.
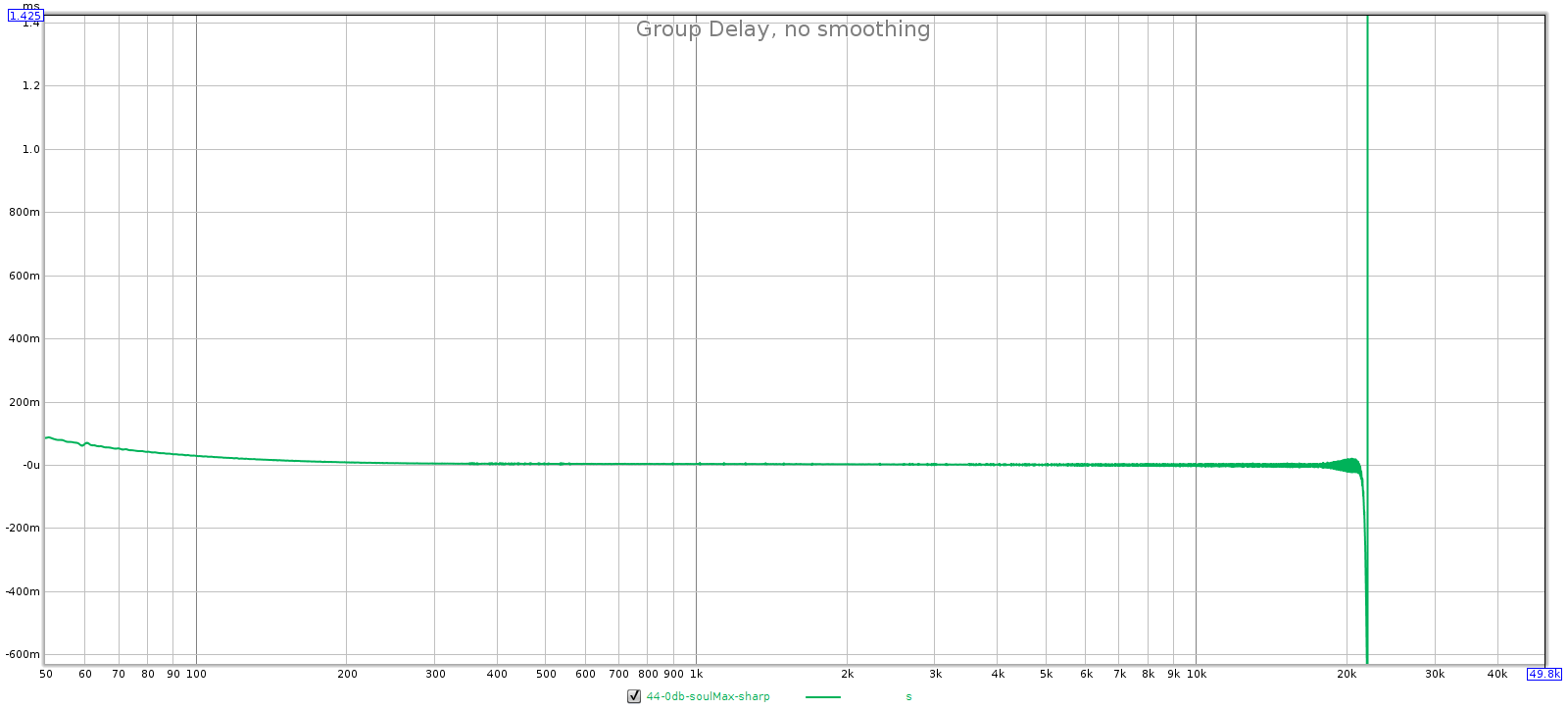
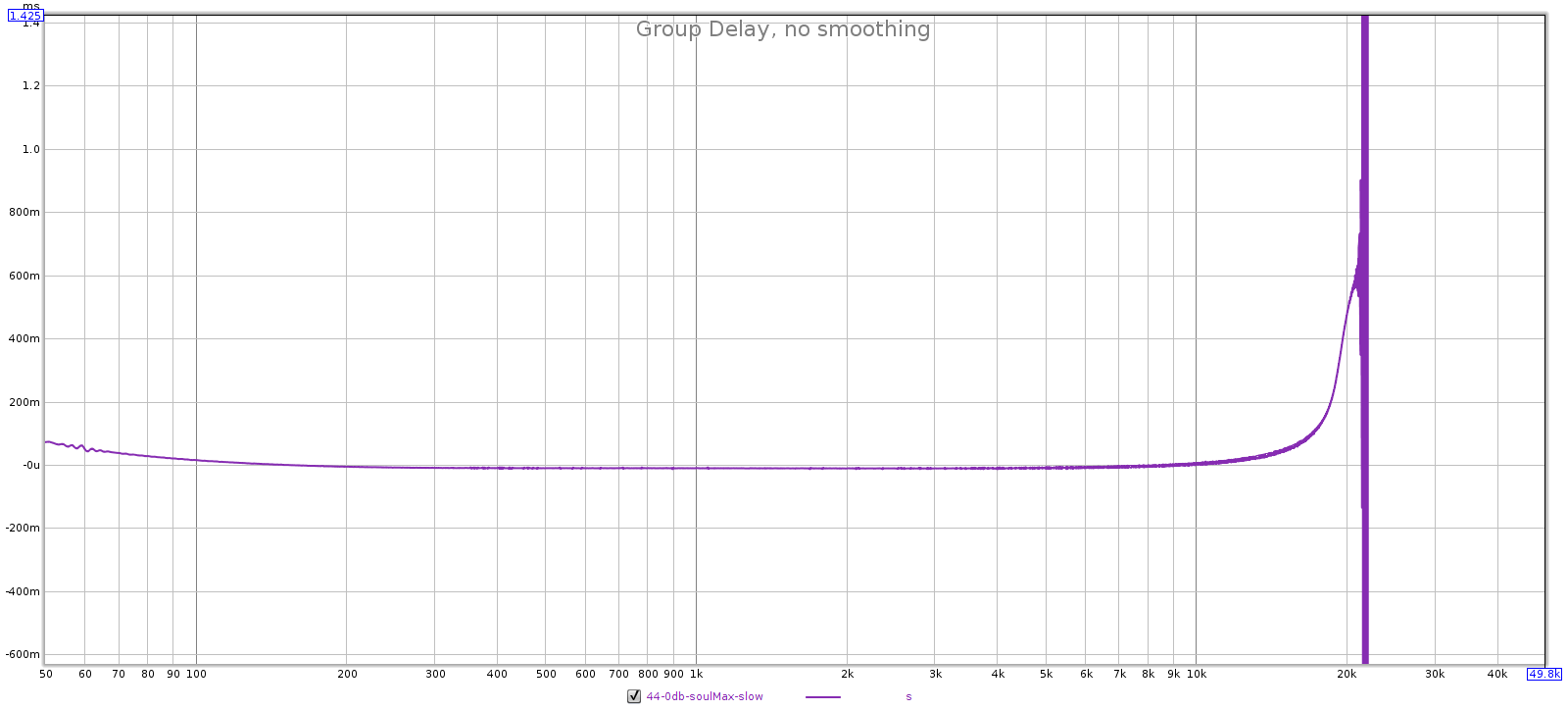
- Group delay: sharp is flatter than slow.
- At high sampling rates, the difference between the filters becomes immaterial. This is consistent with theory.
44.1 kHz: sharp is filter 3 and slow is filter 4.
- Sharp FR doesn’t taper until past 20k, so it must be filter 1 or 3.
- Sharp has flat GD, so it must be filter 3.
- Slow FR tapers past 19k, so it must be filter 4 or 5.
- Slow has more GD than sharp, so it must be filter 4.
48 kHz: sharp is filter 3 and slow is filter 4, for the same reasons as above.
88.2 kHz: Sharp is filter 2 and slow is filter 1.
- Both FR start to taper at 20 kHz, so neither can be filter 3.
- Both have a stopband at 44,100 kHz (beyond 40k), so neither can be filter 4 or 5.
- Sharp has flatter phase / less group delay, which is filter 2.
96 kHz: Sharp is filter 2 and slow is filter 1.
- Both FR start to taper at 20 kHz, so neither can be filter 3.
- Both have a stopband at 48 kHz (beyond 44k), so neither can be filter 4 or 5.
- Sharp has flatter phase / less group delay, which is filter 2.