Background

Most of the sounds we hear are made up of many different frequencies all vibrating together at the same time. The energy in a wave depends on its amplitude and frequency. The higher the amplitude, the more energy. Also the higher the frequency, the more energy. The amplitude part of this makes intuitive sense. The frequency part does too, but it is less obvious.

If the energy of a wave depends on its amplitude and frequency, this implies that if total energy is constant for all frequencies, then amplitude must drop with frequency.

Consider a musical instrument playing a sound. Since energy depends on amplitude and frequency, if it puts equal energy into all the frequencies it emits, then the higher frequencies must have a smaller amplitude. Musical instruments don’t actually put equal energy at all the frequencies they emit, but this does hold true roughly or approximately. If you do a spectrum analysis, they are loudest at or near the fundamental (lowest) frequency and their amplitude drops with frequency. Typically, roughly around 6 dB per octave. That is, every doubling of the frequency roughly halves the amplitude.

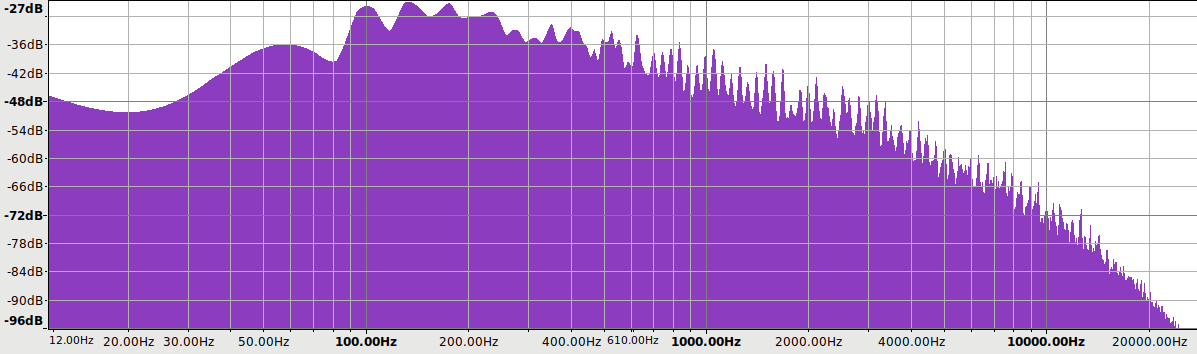
For example, here is amplitude vs. frequency for a high quality orchestral recording:

This graph shows amplitude dropping as frequency increases. Since energy is based on amplitude and frequency, this means roughly constant energy across the spectrum (all frequencies).

This implies that low frequencies are responsible for most of the amplitude in a musical waveform. So, if you look at a typical musical waveform, it looks like a big slow bass wave with ripples on it. Those ripples are the higher frequencies which have smaller amplitudes. Further below I have an example picture.

Audio Linearity

Audio devices are not perfectly linear. They are usually designed to have the best linearity for medium level signals, and as the signal amplitude approaches the maximum extremes they can become less linear. This is generally true with analog devices like speakers and amplifiers, and to a lesser extent with digital devices like DACs.

For example, consider a test signal like 19 and 20 kHz played simultaneously. If you encode this signal at a high level just below clipping, it’s not uncommon for DACs to produce more distortion than they do for the same signal encoded just a little quieter. I’ve seen much smaller level changes, like a 1 dB reduction in level giving a 24 dB reduction in distortion! The same can be true for amplifiers.

Incidentally, when companies publish specs for DACs or CD players, they typically measure distortion at around -20 dB. Yet they measure noise or SNR at full scale. So they’re not really telling the whole truth.

Furthermore, the lower the level of a sound, the fewer bits remain to encode it. 16-bit audio refers to a full scale signal. But a signal at -36 dB has only 10 bits to encode it because the 6 most significant bits are all zero. Because in music the high frequencies are at lower levels, they are encoded with even fewer bits, which is lower resolution. In our -36 dB example, high frequencies 3 octaves above the fundamental are likely 18 dB smaller, which is only 7 bits. When we consider that the lowest bit is dither, this is only 6 bits for the frequencies where our hearing is most sensitive!

The Redbook CD standard had a solution to this called pre-emphasis: boost the high frequencies before digital encoding, then cut them after decoding. This was an effective solution but is no longer used because it reduces high frequency headroom and most recordings today are made in 24 bit and are dithered when converted to 16-bit.

The Importance of Bass Response

One insight from the above is that bass response is more important than we might realize. At low frequencies (say 40 Hz), the lowest level of distortion that trained listeners can detect is around 5%. But at high frequencies (say, 2 kHz), that threshold can be as low as 0.5%.

So one could say who cares if an audio device isn’t perfectly linear? Because of the energy spectrum of music, the highest amplitudes that approach non-linearity are usually in the bass, and we’re 10 times less sensitive to distortion in the bass, so we won’t hear it.

But this view is incorrect. It is based on faulty intuition. The musical signal is a not a bunch of frequencies propagating independently. It is a single wave with all those frequencies superimposed together. Thus, the high frequencies are riding as a ripple on the bass wave. If the bass wave has high amplitude approaching the non-linear regions of a device, it is carrying the smaller amplitude high frequencies along with it, forcing even those smaller frequencies into the non-linear region.

A picture’s worth 1,000 words so here’s what I’m talking about, a snippet from a musical waveform. The ripples marked in red are the midrange & treble which is lower amplitude and normally would be centered around zero, but riding on top of the bass wave has forced them toward the extreme positive and negative ranges:

Speaker Example

Here’s another practical example. Decades ago, I owned a pair of Polk Audio 10B speakers. They had two 6.5″ midrange drivers, a 1″ dome tweeter, and a 10″ tuned passive radiator. The midrange drivers produced the bass and midrange. As you turned up the volume playing music having significant bass, at some point you started hearing distortion in the midrange. This is the point where the bass energy is driving the 6.5″ driver excursion near its limits where its response goes non-linear. All the frequencies it produces are more or less equally affected by this distortion, but our hearing is more sensitive in the higher frequencies so that’s where we hear it first.

Obviously, if you turn down the volume, the distortion goes away. However, if you use EQ or a tone control to turn down the bass, the same thing happens – the distortion goes away. Here the midrange frequencies are just as loud as before, but they’re perfectly clear because the distortion was caused by the larger amplitude bass wave forcing the driver to non-linear excursion.

Other Applications: Headphones

The best quality dynamic headphones have < 1 % distortion through the midrange and treble, but distortion increases at low frequencies, typically reaching 5% or more by the time it reaches down to 20 Hz. The best planar magnetic headphones have < 1% distortion through the entire audible range, even down to 20 Hz and lower. This is due in part to having a physically large driver, which moves less to produce a given volume level.

Most people think it doesn’t matter that dynamic headphones have higher bass distortion, because we can’t easily hear distortion in the bass. But remember that the mids and treble are just a ripple riding on the bass wave, and most headphones have a single full-range driver. If you listen at low levels, it doesn’t matter. But as you turn up the volume, the bass distortion will leak into the mids and treble and become audible.

Thus, low bass distortion is more important in a speaker or headphone, than it might at first seem. If the headphone or speaker has a separate bass driver with a crossover, then this doesn’t apply – the mids and treble aren’t affected by the bass excursions.

Test signals like frequency sweeps will not show this increased distortion, because they don’t play bass & treble at the same time.

Other Applications: amplifiers and DACs

Amplifiers and DACs have a similar issue, though to a lesser extent. This concept applies here as well – especially when considering the dynamic range compression that is so often applied to music these days.

Consider a digital recording that is made with dynamic range compression and leveled too hot, so it has inter-sample overs or clipping. Or, it may be perfectly clean, but with levels that are just below full scale. Sadly, this describes most modern music rock/pop recordings, though it’s less common in jazz and classical.

Most of the energy in the musical waveform is in the bass, so if you attenuate the bass you reduce the overall levels by almost the same amount. This will entirely fix inter-sample overs, though it can’t fix clipping. Remember the 19+20 kHz example above, showing that distortion increases as amplitude levels approach full scale? With most music, attenuating the bass will fix that too, since the higher frequencies are usually riding on that bass wave. For example, this explains how the subsonic filter on an LP may improve midrange and treble response.