For background, here is part 1. It introduces slide rules and covers basic usage with C, D and CI scales. Here we cover the A, B and K scales for squares, square roots, cubes and cube roots.
A Scale: Squares and Square Roots
The A scale shows the square of each number on the D scale. Conversely, the D scale shows the square root of each number on the A scale.
Below the cursor shows that 3 on the D scale matches 9 on the A scale.

Note that as the D scale goes from 1 to 10, the A scale goes from 1 to 100. This means every single-digit number in the A scale has a corresponding double-digit number further up the scale. That is: 1 and 10, 2 and 20, 3 and 30, etc.
For example, below the cursor is on the A scale 30, showing the square root of 30 is 5.48:

So, squares are easy: just find the number on D scale and look to the corresponding number on A scale. But going the opposite direction, square roots, becomes ambiguous. What if you want the square root of a number that is not in the range of 1 to 100? For example:
- If you want the square root of 400, on the A scale do you use 4 or 40?
- If you want the square root of 4000, on the A scale do you use 4 or 40?
- If you want the square root of 0.5, on the A scale do you use 5 or 50?
First, observe that all of the single-digit numbers in the A scale occupy the first half, all the double-digit numbers the second half, and the split (the value 10) is exactly the mid-point of the scale. Thus, you can think of the A scale has having 2 halves. So the question boils down to knowing which half to use.
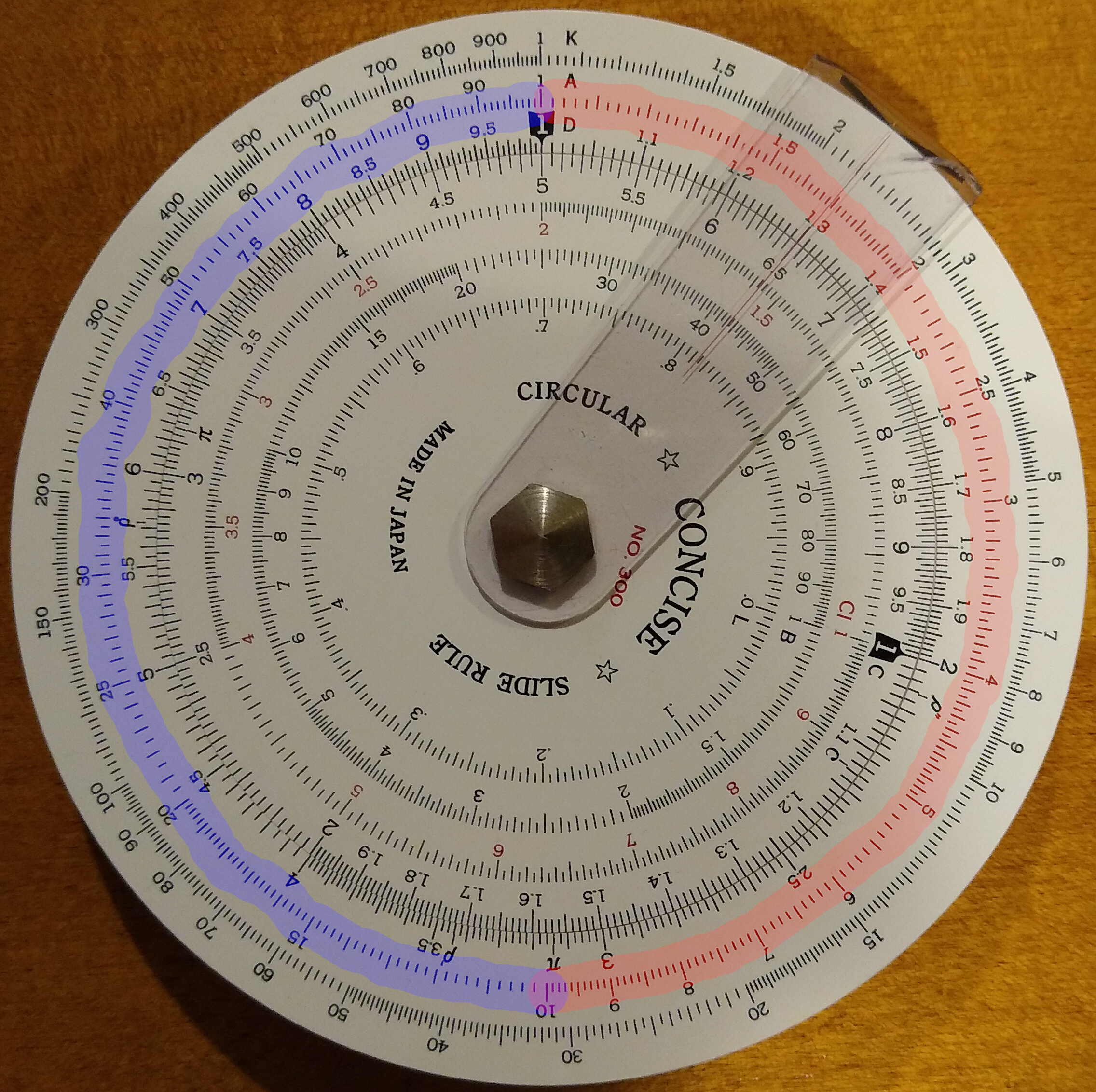
The answer is based on how many zeroes in the number whose root you want to know: is that number of zeroes odd or even? Adding or removing each zero (or each decimal point shift left or right) shifts back and forth between the 2 halves of the scale.
For example, consider the number 4.
- The square root of 4 is 2 (low side of A scale).
- The square root of 40 is 6.32 (high side of A scale).
- The square root of 400 is 20 (low side of A scale).
- The square root of 4000 is 63.2 (high side of A scale).
This pattern simply repeats. And it also repeats in the opposite direction:
- The square root of 0.4 is 0.632 (high side of A scale).
- The square root of 0.04 is 0.2 (low side of A scale).
- The square root of 0.004 is 0.0632 (high side of A scale).
K Scale: Cubes and Cube Roots
The K scale works like the A scale. To cube any number N, find N on the D scale and look at the corresponding number on the K scale.
For example, this shows that 2 cubed is 8 (it actually shows that 2 squared is 4, and cubed is 8):

Yet the K scale also has the value 80, whose cube root is 4.31:

And the K scale also has the value 800, whose cube root is 9.28:

So while the A scale splits into 2 equal parts (1-10 and 10-100), the K scale splits into 3 equal parts: 1-10, 10-100, and 100-1000. Each of these occupies exactly 1/3 of the scale:
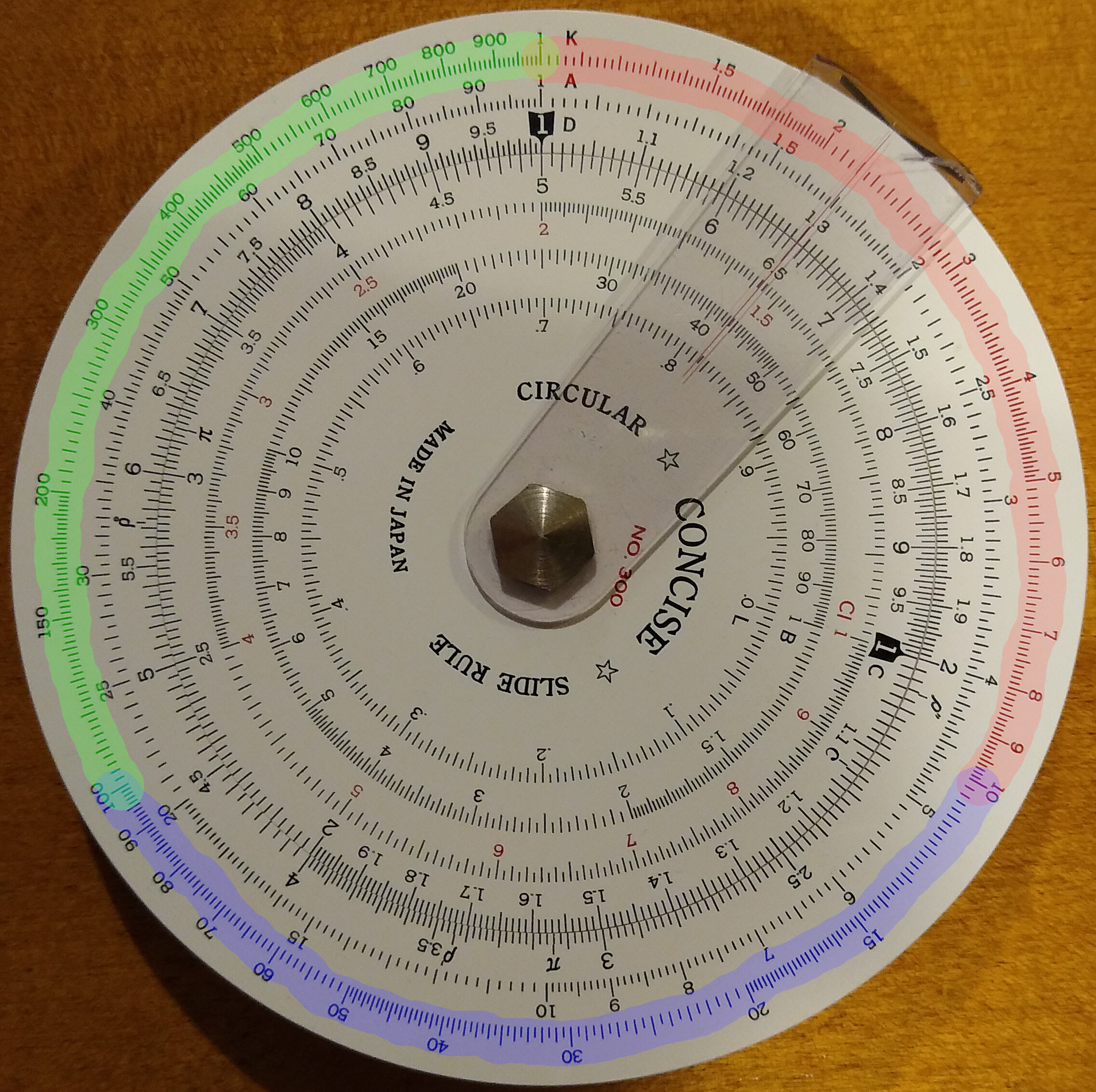
As with the A scale, cubing numbers is simple. Find N on the D scale and the corresponding K scale is N cubed. Yet doing the opposite, taking the cube root, is a bit more complex. You need to know which 1/3 of the scale to use. The procedure is a simple extension of what we did for the A scale. Yet since the A scale had only 2 parts, we thought of it as flipping back and forth. With the K scale having 3 parts, instead of flipping, each shift of the decimal point rotates forward to the next, or back to the prior part of the scale.
For example, consider the number 8:
- The cube root of 8 is 2 (part 1 of K scale).
- The cube root of 80 is 4.31 (part 2 of K scale).
- The cube root of 800 is 9.28 (part 3 of K scale).
- The cube root of 8000 is 20 (part 1 of K scale).
It repeats every 3rd shift of the decimal point. And it also applies in the reverse direction as numbers get smaller:
- The cube root of 0.8 is 0.928 (part 3 of K scale).
- The cube root of 0.08 is 0.431 (part 2 of K scale).
- The cube root of 0.008 is 0.2 (part 1 of K scale).
Exponents and Roots other than 2 or 3
Most everyday problems, especially those involving basic physics, use squares or cubes. Powers other than 2 or 3 are uncommon. Yet we do occasionally encounter them and you can solve them with a slide rule. The trick is to know some basic math rules about adding exponents.
Suppose we some number N, say 3.5, and we want to know N to some power, say the 7th power. So how would we compute 3.5^7 with our slide rule?
First, we split the exponent into smaller parts involving squares and cubes:
3.5^7 = 3.5^(2+2+3)
Next we split this out:
3.5^(2+2+3) = 3.5^2 * 3.5^2 * 3.5^3
Now we have split the problem into squares and cubes so we can compute it on our slide rule:
3.5^2 = 12.2 3.5^3 = 42.8 12.2 * 12.2 * 42.8 = 150 * 42.8 = 6,430
Checking this with a calculator, I get 6,433.9. The slide rule gave us 3 significant figures.
Note: you can apply this same method with roots by taking the exponents as fractions. That is, the square root of 2 is 2 to the 1/2 power, cube root of 2 is 2 so the 1/3 power, etc.
What About that B Scale?
The B scale is the same as the A scale, used for squares and square roots. But it corresponds with the C scale instead of the D scale. Using D-A is the same as C-B. The B scale isn’t essential, but it is sometimes useful. On the Concise model 300, the A scale is along the outer circumference and the B scale is further inside. This makes the A scale longer and more accurate.

To quantify, on this Concise model 300 the A scale has a diameter of 9.2 cm and B scale 5.9. The A scale is 9.2 / 5.9 = 1.56 times longer. That’s a significant difference!
Conclusion
With squares and cubes, the power of the slide rule increases and we can solve a wider variety of problems. The next step is trigonometry: sine, cosine, tangent. These come up frequently in simple physics and everyday problems. This is covered in part 3.