Introduction
After I had to return my 2nd piece of Chi-Fi equipment due to poor build quality and support, I said I was done with Chi-Fi and would stick to other manufacturers. However, after Amir reviewed the Topping E70 on ASR, I couldn’t resist. A fully balanced DAC among the best and cleanest he has ever measured, for $350 would be too good to be true.
My Corda Soul is a DAC, preamp, headphone amp, and DSP processor. Of these functions, most are SOTA quality except for its DAC. It uses dual WM8741 chips which were great for 2007, but DAC technology has improved.
The topping E70 is a line level DAC and nothing more. That is:
- DAC using ESS 9028 Pro chips
- Analog outputs: both balanced/XLR and single ended/RCA
- Inputs: SPDIF (coax and toslink), USB, and Bluetooth
- Internal power supply
- Digital volume control
- Display showing sample rate and output level
- High build quality with a metal case
- Excellent measured performance, among the best at ASR
Setup
I measured the E70 and the Soul using my Tascam DA3000, which has excellent DA and AD converters. Better than my Juli@ sound card, but not as good as an APx555. This would later lead to a surprise due to misleading measurements…
The Corda Soul distortion profile has always looked like this (Room EQ Wizard Sweep at 48 kHz):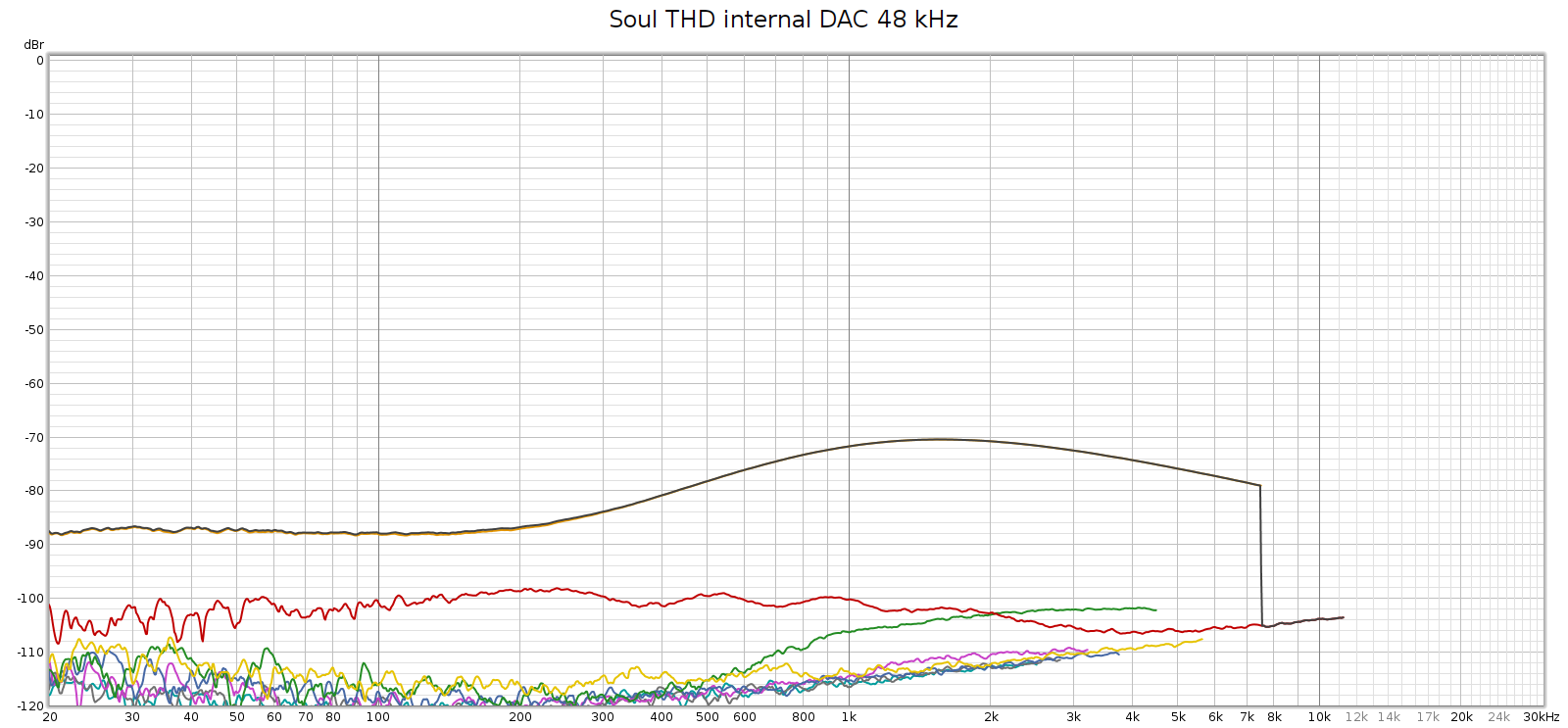
You can see above that noise is excellent (too low to be measured) and distortion is generally good at -100 dB, but 3rd harmonic is not so good, rising to -70 dB in the upper mids.
I never knew where exactly this 3H hump came from: the Soul’s digital stage, analog stage, or DA conversion. I recently discovered that it comes from DA conversion. More on that here. I set up the Soul to use the E70 as an external DA converter (it can do that!) and here is how it measured:
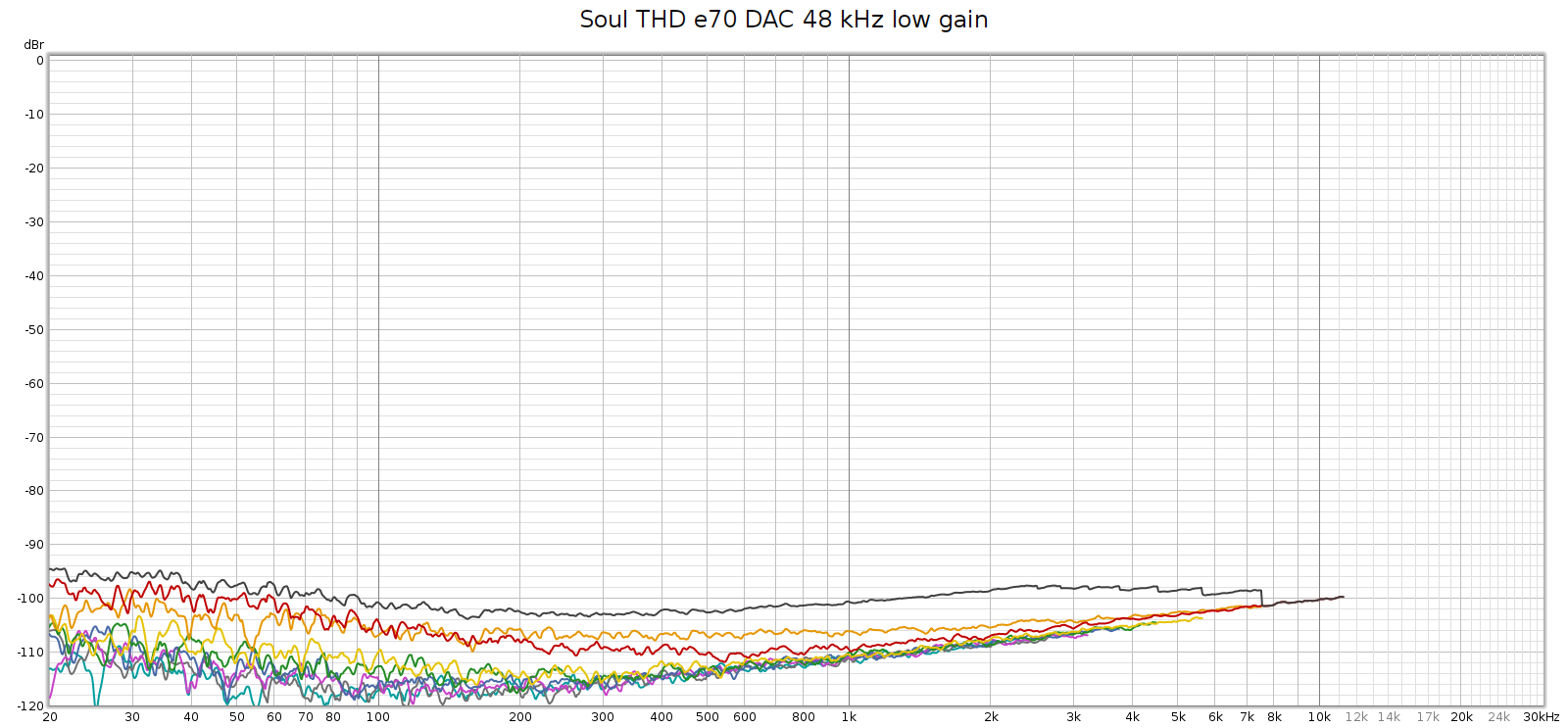
So ends the story, right? That’s what I thought, until I measured it at 192 kHz.
High Frequency Noise
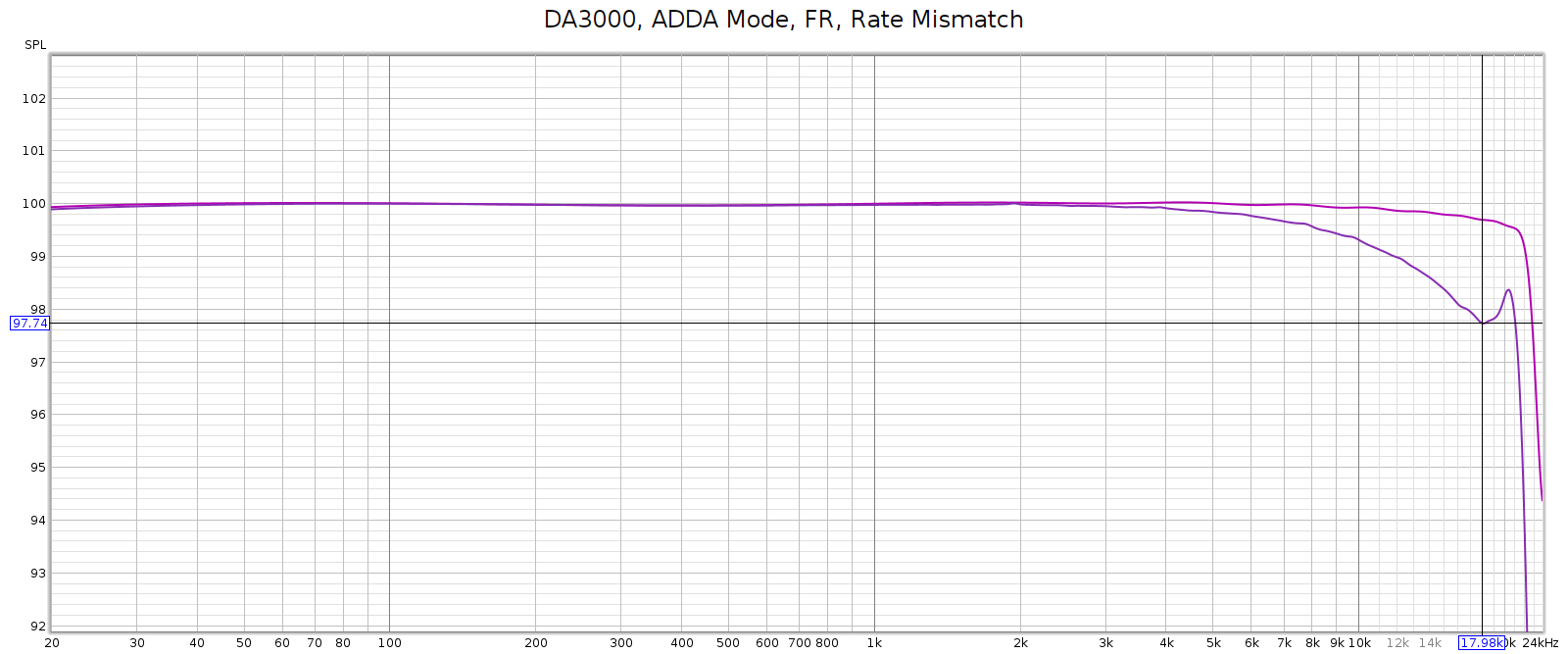
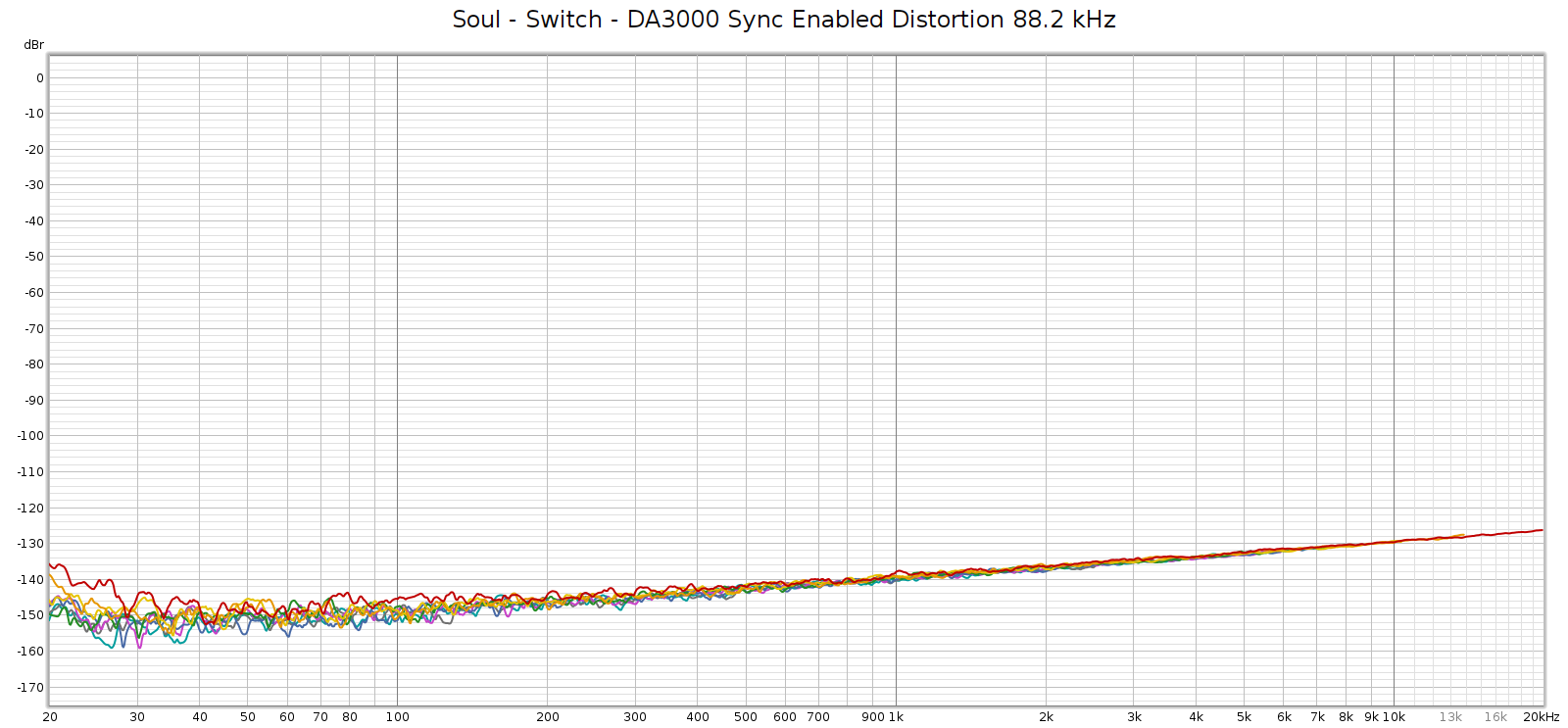
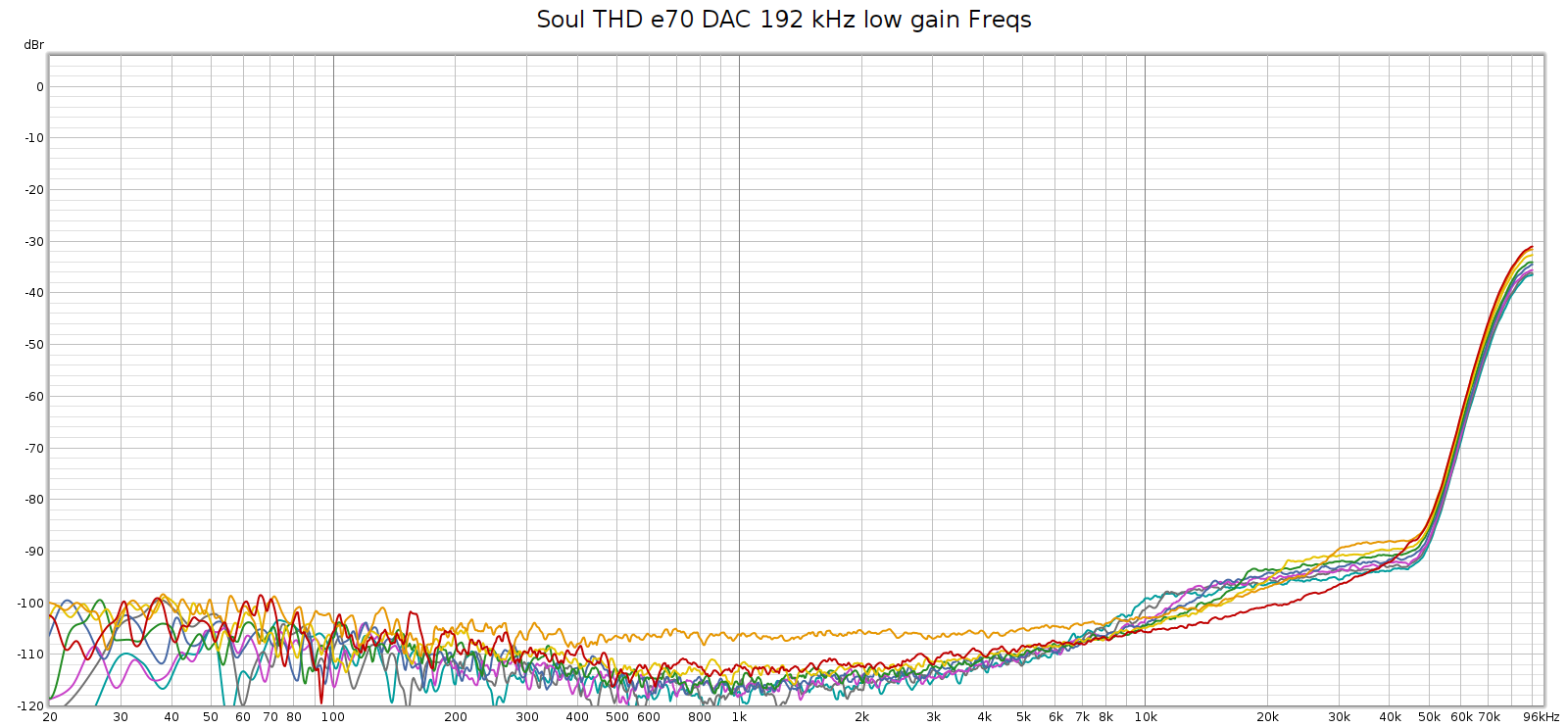
The Soul always had a noisier sweep at 192 kHz, like this:
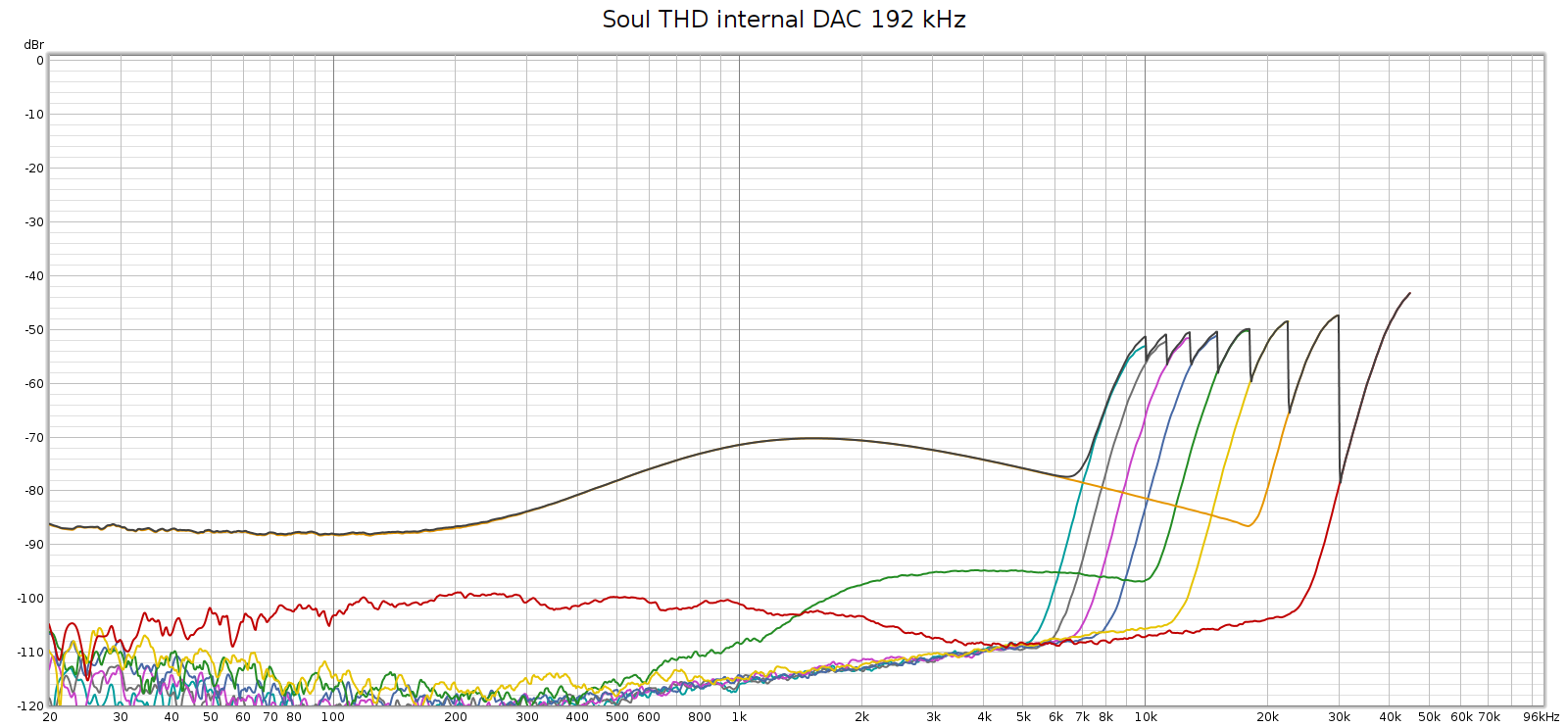
Each of those distortion plots peaks at the same frequency:
- 2H (red) at 45 kH, and 2 * 45 = 90
- 3H (orange) at 30 kH, and 3 * 30 = 90
- 4H (yellow) at 22.5 kHz, and 4 * 22.5 = 90
- etc.
So the plot is misleading. What’s actually happening is that there is HF noise at 90 khz, and the plot is interpreting it as if it were harmonics of lower frequencies – in other words, harmonic distortion. Thus, I assumed this was due to high frequency noise from its switching power supplies not being properly suppressed.
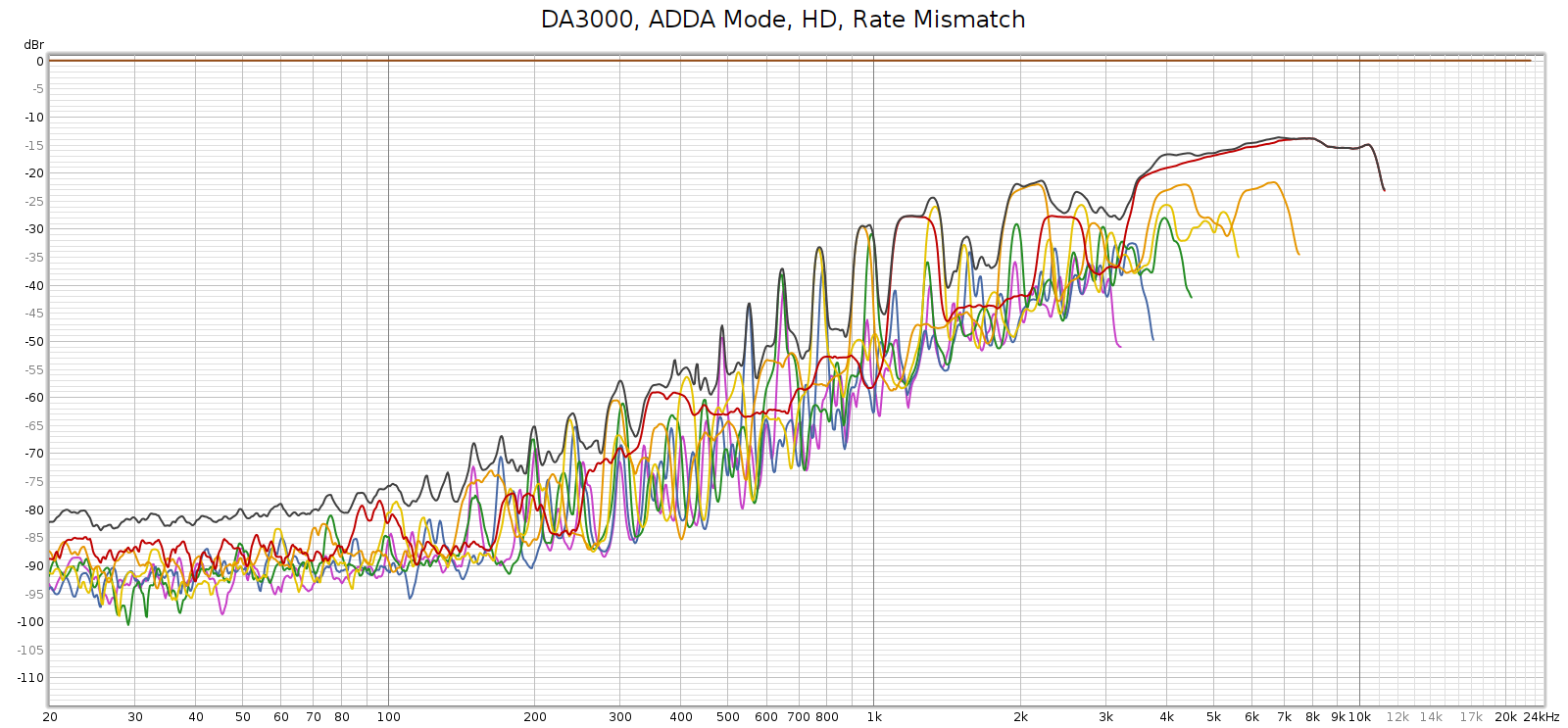
Here’s a different perspective on that same plot, plotting harmonics at their native frequency, which makes the above interpretation obvious:
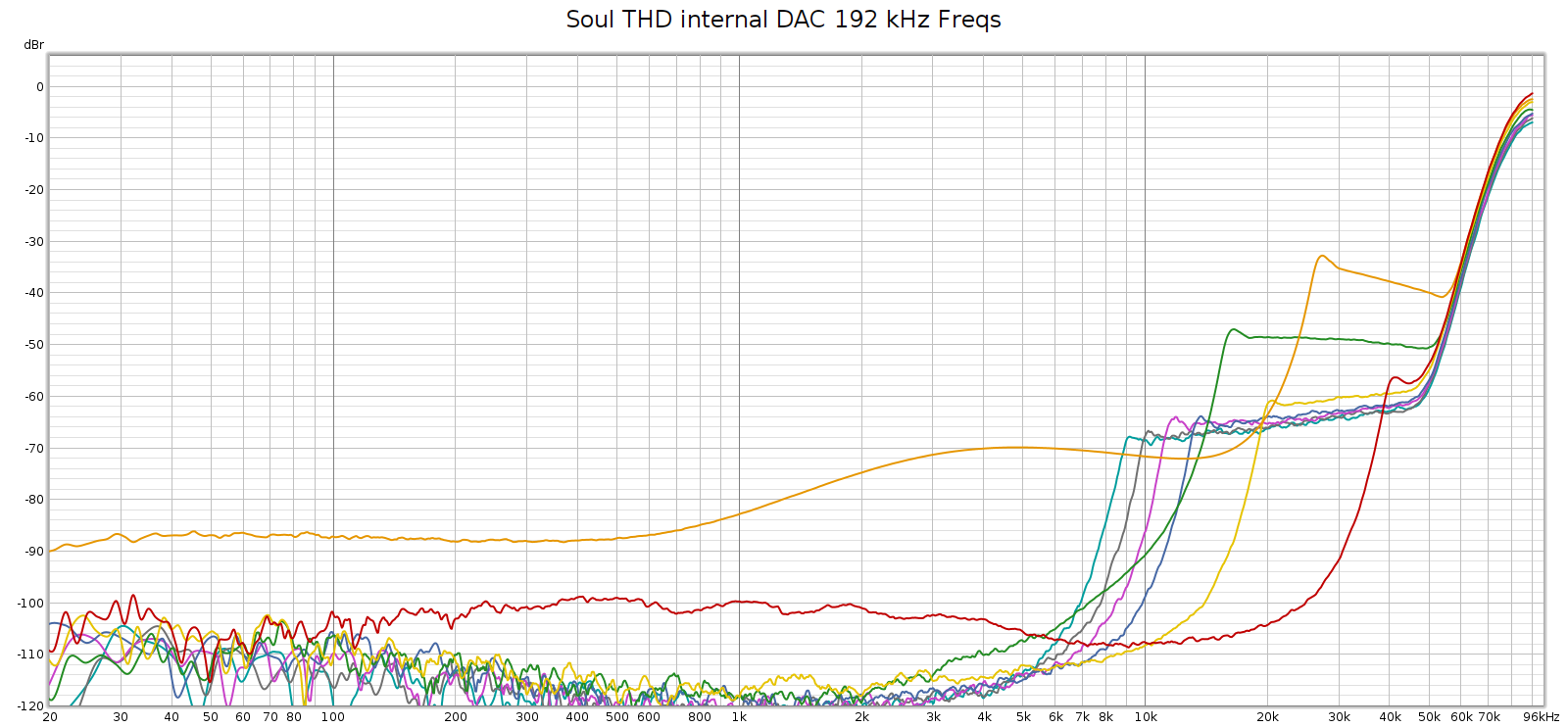
But, the Soul’s power supplies (Meanwell IRM-20-24) switch at 65 kHz, not at 90 kHz. So where was that noise coming from? Maybe it wasn’t coming from the Soul at all.
Process of Elimination
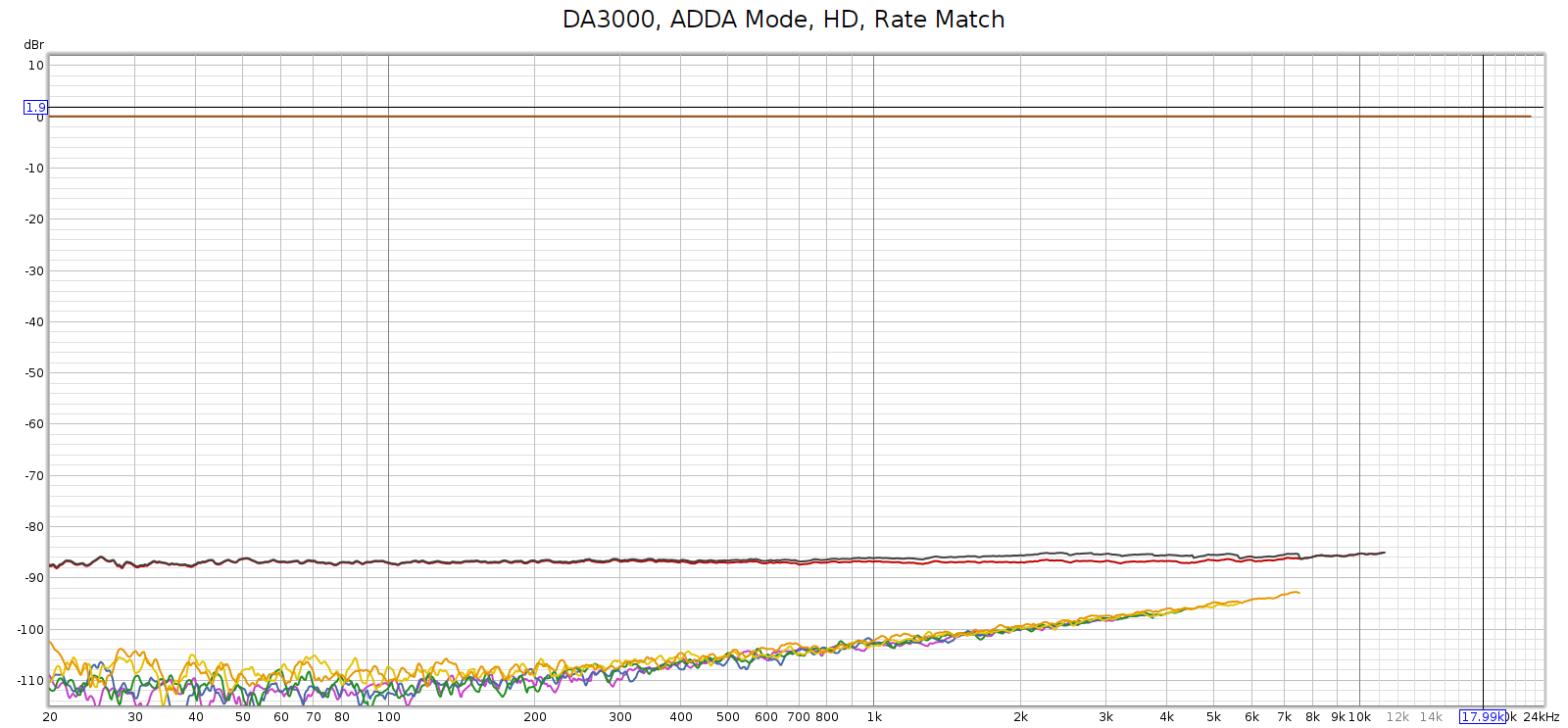
I connected the E70 balanced analog outputs directly to the Tascam DA3000 inputs and recorded a 192 kHz sweep. Here’s what I got:
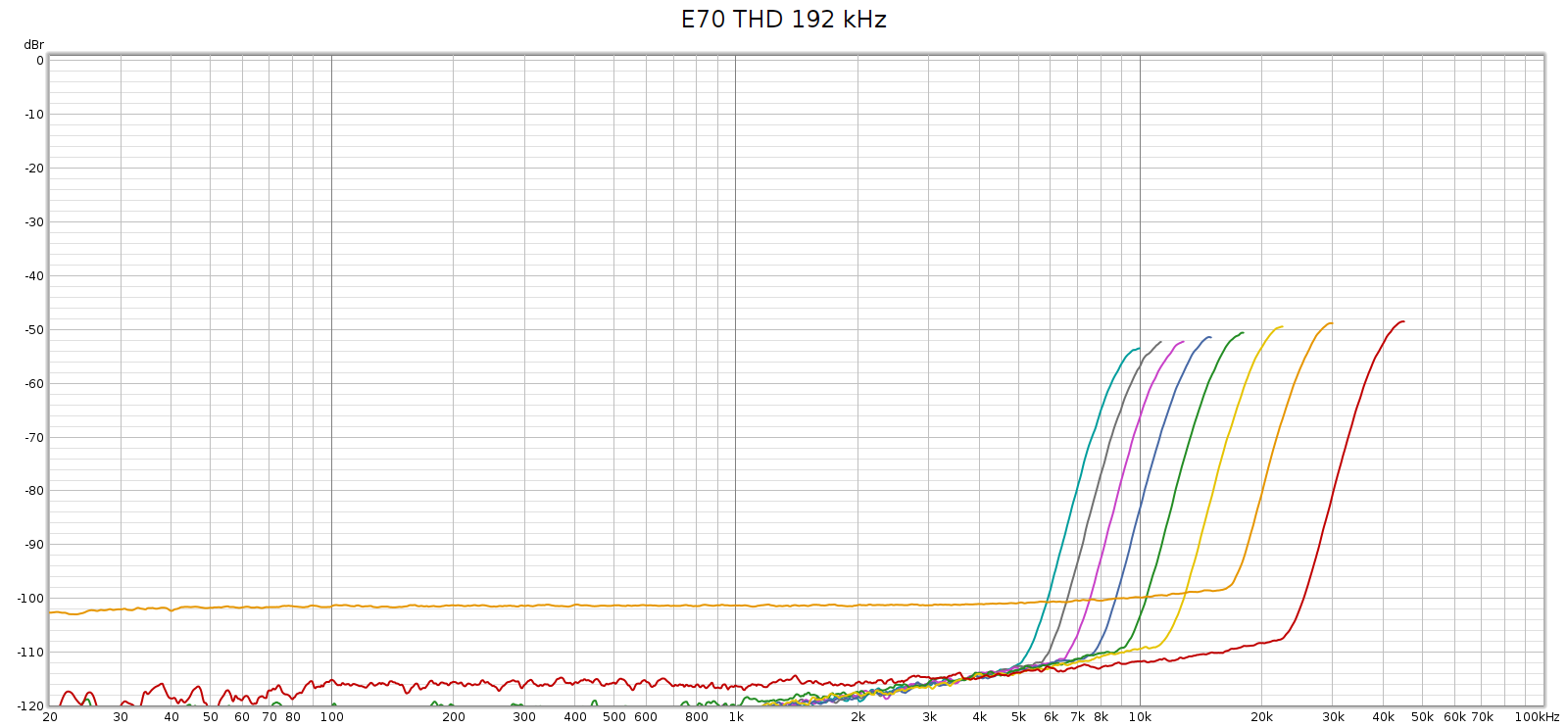
Or, looking at this plot the other way:
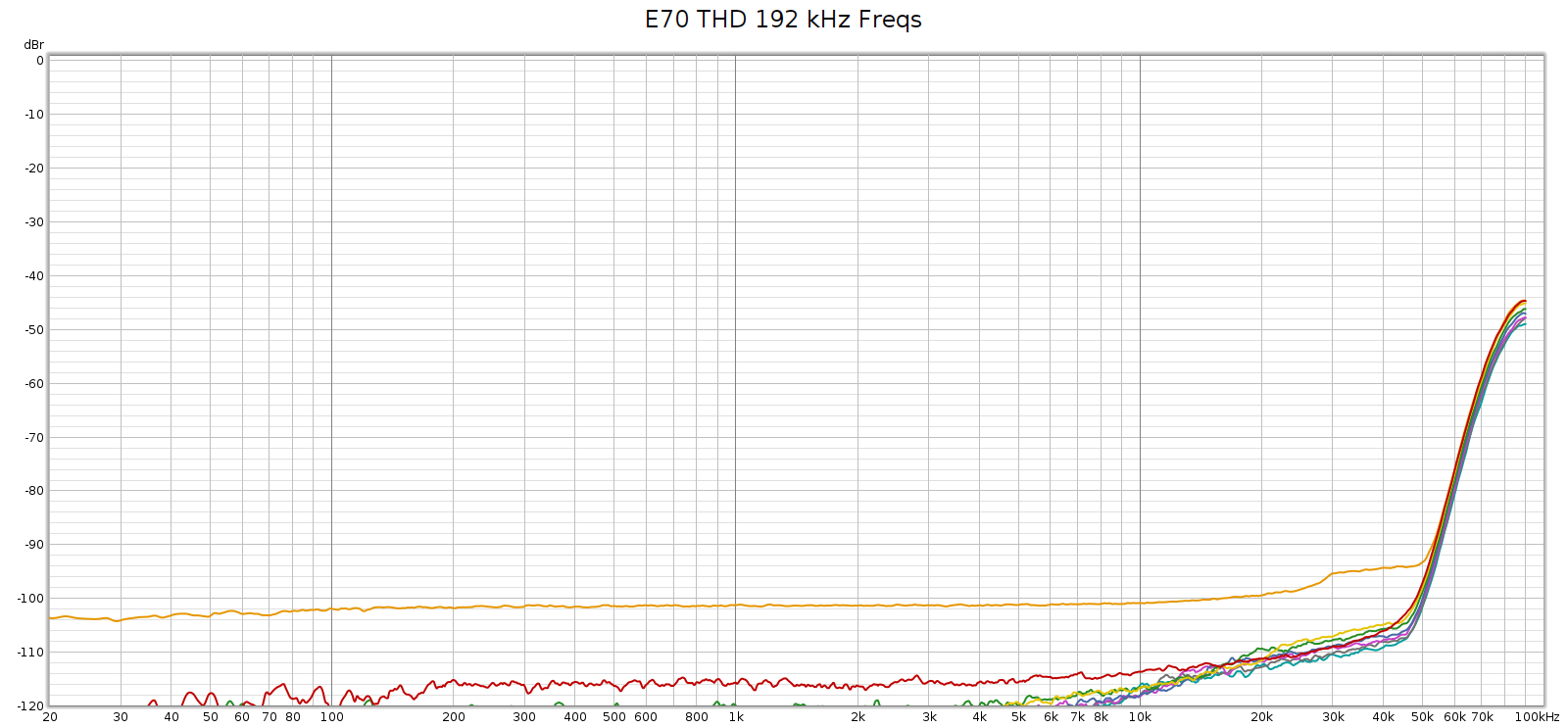
So that HF noise wasn’t coming from the Soul.
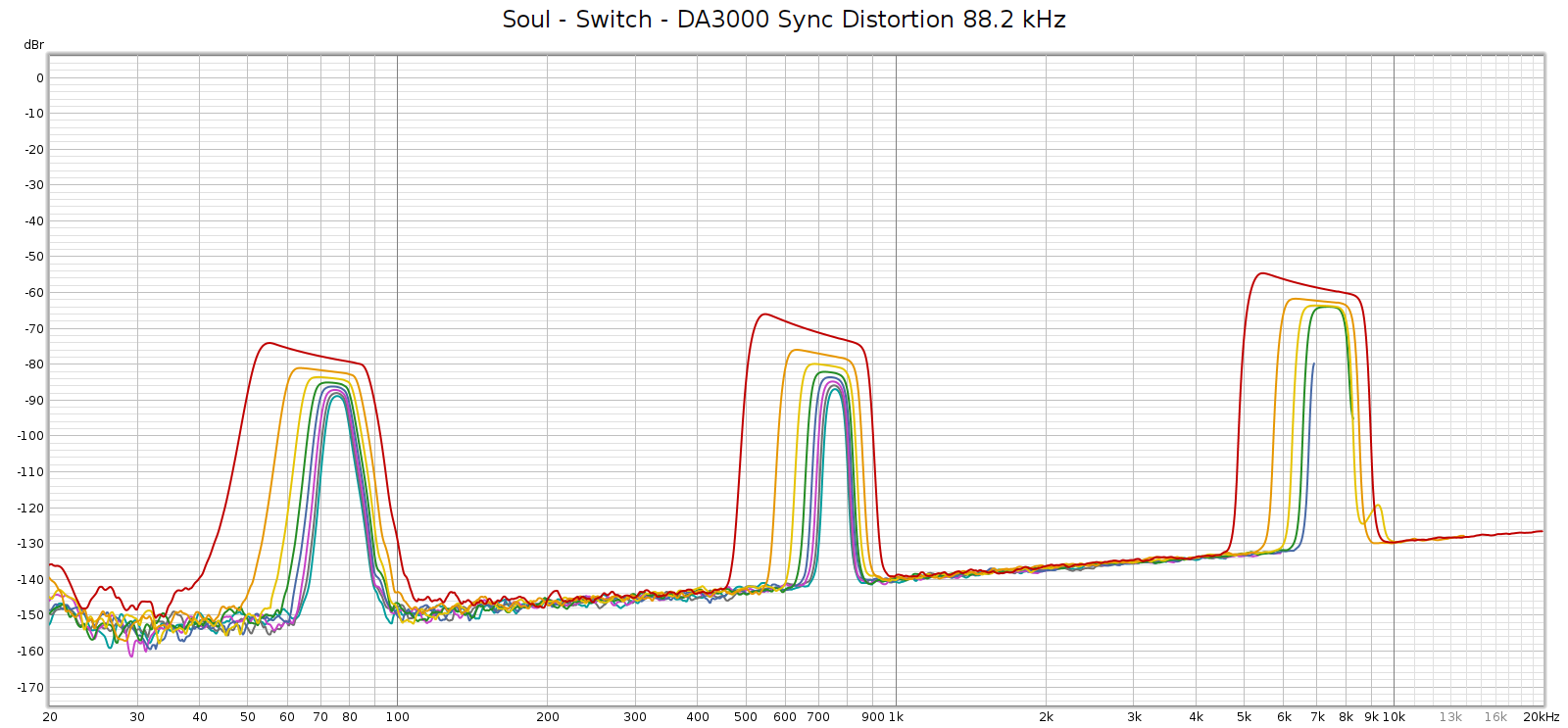
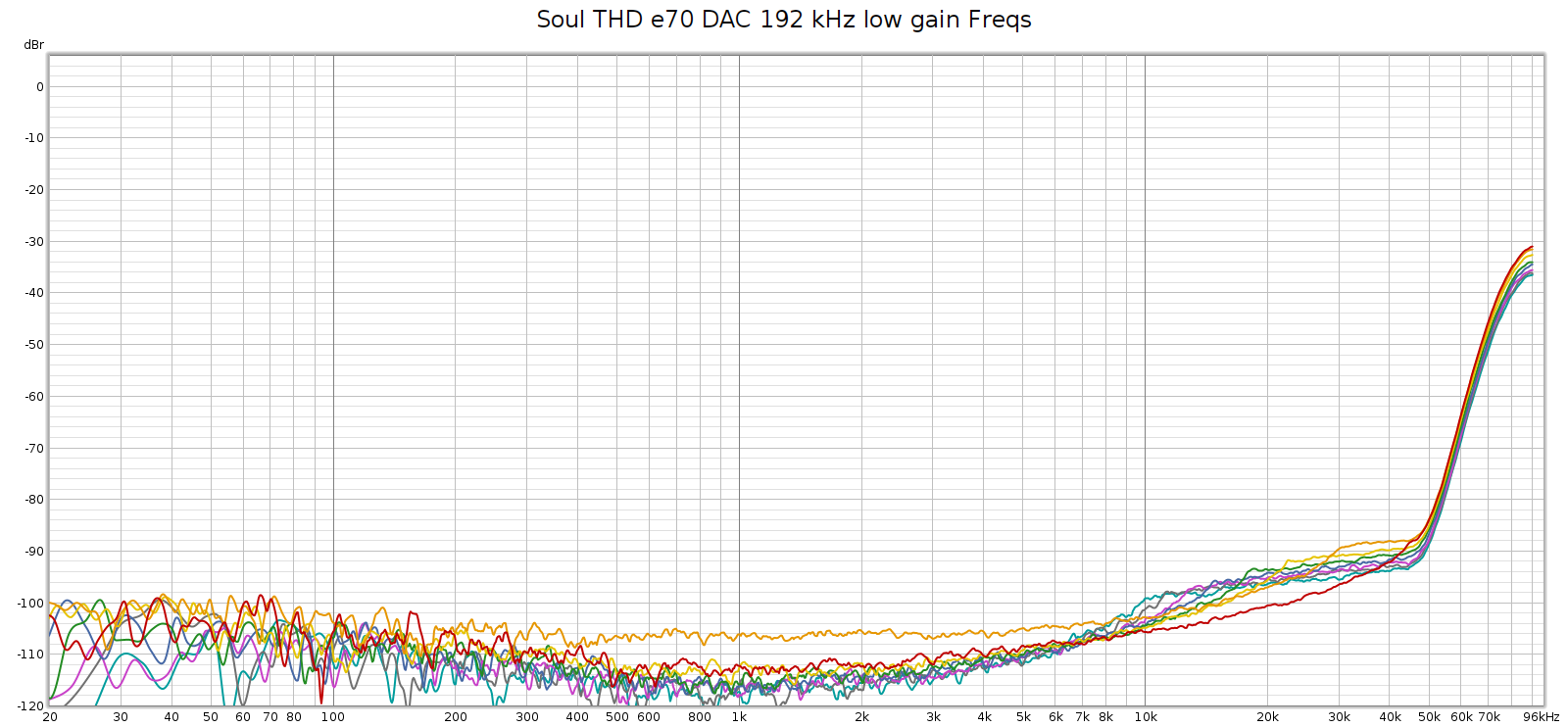
Next, I measured the Soul at 192 kHz using the E70 as its external DAC:
It’s essentially the same as the E70 direct, same shape just a few dB higher as it’s passing through an additional analog stage.
Setup – Conclusion
What I learned is that HF noise around 90 – 100 kHz is created by the Tascam recorder. When you record from its analog inputs, the signal passes through its A/D converters which introduce this noise, probably from a system clock or switching power supply. This noise is only at sample rates of 176.4 kHz and higher, because at lower rates, it’s above the Nyquist frequency so the digital filters kill it.
The E70 DAC is clean at all sample rates including 192 kHz. And the Soul’s analog stage is also clean. The Soul’s internal DA converters are not as clean, adding at bit of distortion at midrange-treble frequencies in the audible band. Thus, the Topping E70 addresses the Corda Soul’s relative weak point, and the combination gives truly SOTA audio reproduction.
One might ask why not simply use the E70 to directly drive my power amp? Why use the Soul at all?
- The Soul serves as a convenient preamp, having multiple digital inputs.
- The Soul has unique and valuable DSP functions: tone controls, headphone crossfeed, etc.
- The Soul’s volume control is an analog stepped attenuator gain switch that is mechanically reliable and ultra clean with perfect channel balance at all settings.
- The E70’s volume control is software which can glitch or lose memory, causing instant power spikes damaging speakers.
- The Soul’s analog stage is clean and transparent, so there is no downside to its value and convenience.
- Reliability and durability: the Soul is built like a rock by Lake People in Germany, well beyond Chi-fi quality standards.
- Redundancy: if the E70 (or any other external DAC that I use) ever dies, I can use the Soul as a complete system while getting the DAC repaired or replaced.
E70 Review
Setup issues resolved, let’s return to the E70 review. It’s a simple black box with minimal controls:
- Power switch on the rear left side
- Rotary knob / button on the front right side
- Capacitive touch button on the front left side
Features and Observations
You can leave the power switch on all the time and it will automatically power up and down as it detects a digital input signal.
You can set its output level to 4V (standard unbalanced) or 5V, which is about 2 dB louder with consequently higher SNR. 5 Volts may be too much for some devices, so make sure it is compatible. However, if this is the case, I recommend using 5 V anyway and setting the digital volume to -2 or -3 dB for reasons explained below.
I wish its high voltage output supported 16 V which is standard for professional balanced audio (as the Tascam DA3000 has). But it doesn’t.
It has digital volume control set in software. It might seem there is no reason to set it to anything other than max (0 dB). Yet setting it to -2 or -3 dB should give more headroom to better decode digital audio that is recorded too hot with intersample overs or clipping.
When the digital volume control is enabled, the display shows only the volume level, not the current sample rate. When disabled (always output max volume), the display always shows the current sample rate. I wish this were configurable. I’d like to enable digital volume and see the current sample rate.
The display can be configured to go dark and light up only when the knob is used. This is a nice feature yet it has a little bug described below.
The E70 has 7 different digital filters. Here’s how they measured at 44.1 kHz:
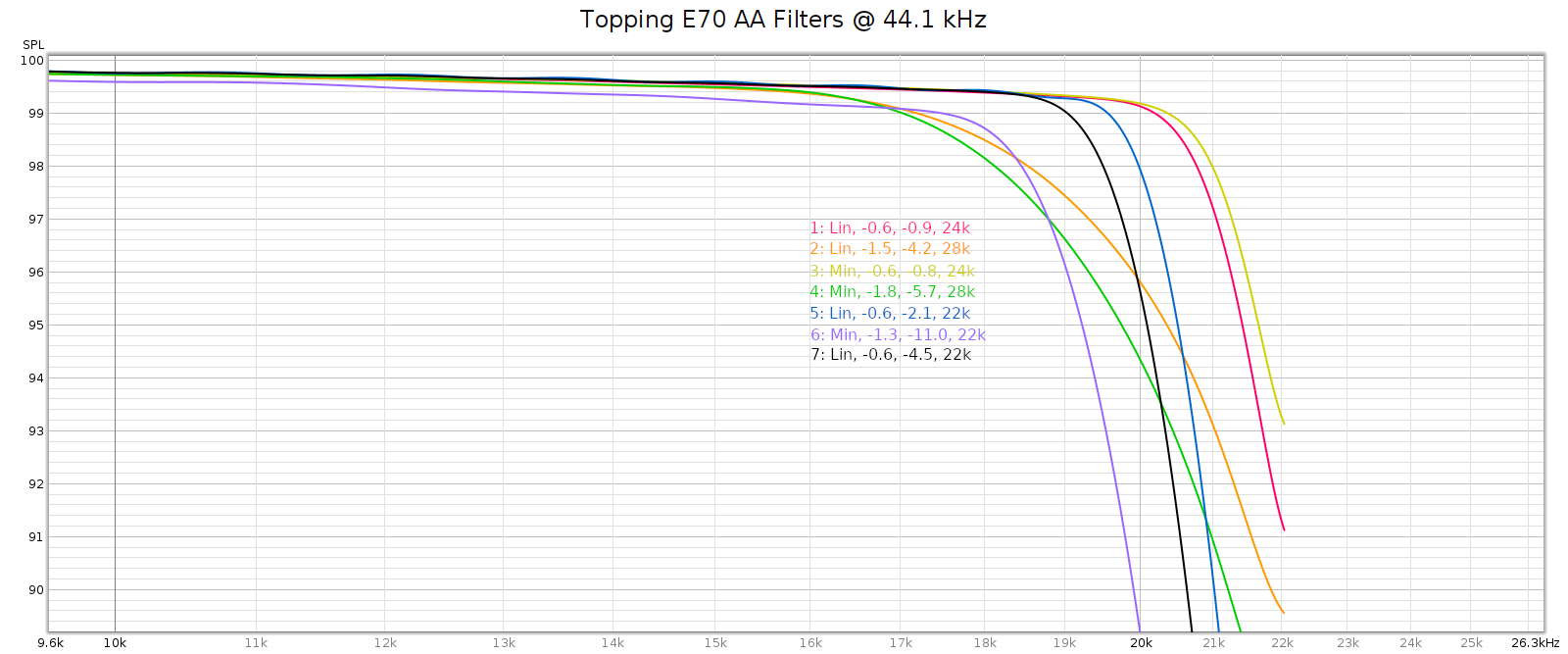
Filter #3 is the default, which is a decent choice. But it is minimum phase, so I switched to filter #1 which has the same response and is linear phase.
Drawbacks & Limitations
Whenever the input sample rate changes, the E70 emits a “click” / “chirp” to the analog outputs. Take care to adjust volume when changing recordings.
If while the display is dark you turn the knob to adjust the volume, the first knob click that wakes up the display changes the volume yet the display shows the prior volume before it changed, so the displayed volume is incorrect.
Firmware 1.04 adds the capability to set SPDIF sample rate lock sensitivity with a new setting called DPLL. This was essential for me because the default DPLL setting 5 didn’t handle 88.2 and 176.4 sampling well, so I upped it to 7 and it became clean. Setting 6 also worked but I figured I’d give it one extra nudge just to be sure. But Topping hasn’t yet put this firmware up on their support site. You can get an unofficial copy at ASR: https://www.audiosciencereview.com/forum/index.php?threads/topping-e70-stereo-dac-review.39188/post-1411763
Sound Quality (Subjective)
When level matched, the E70 is virtually indistinguishable from the Corda Soul’s built-in WM8741 DACs. There is no difference in voicing or frequency response. Yet when playing certain kinds of music there is a slight difference. The E70 better resolves layers of subtle detail in complex orchestral music. In recordings with moderate to heavy reverb/echo, such as from a cathedral, where the music can get drowned or saturated with reverb, it resolves the musical line more clearly. These differences are very subtle, audible with only some kinds of music, and easy to over-state. Yet they can be heard.
In contrast, the Tascam DA3000 in DA-AD mode (DAC only) shows a greater difference. It is voiced slightly warmer than the Soul or E70.
Conclusion
The E70 provides truly SOTA sound quality both subjectively and in measurements. It’s not perfect, having some firmware bugs, and Topping is not known for good support. And the build quality seems good yet long term reliability is unknown. But for the price (about $350) it cannot be beat.