Background
I learned to use slide rules in high school in the 1980s. My physics teacher was one of the most memorable teachers in my life, “Mr. Jordan”. He said that slide rules can be faster than a calculator, and they promote a better understanding of numbers, orders of magnitude, and significant figures. They are not as accurate as calculators, but real-world problems only need 2-3 significant figures. As such, anyone who used a slide rule instead of a calculator would get a bonus 10% on every test, and answers would be considered correct if they were within 1% of correct. I was one of the few who took him up on this offer.
He handed out small circular slide rules, saying they were easier to use than linear slide rules (which is true, since circular never goes off scale). I don’t remember exactly what model slide rule it was, but the closest I know of today is the Concise model 28N. It was either that, or something very similar.
Note: I now have a Concise model 300, which is their biggest and best. The C and D scales are 8 cm in diameter, which is a circumference of 8π which is 25.2 cm, or about 10″. This is the slide used used in the photos below.
All we needed for physics was multiplication and division, and squares & cubes. Jordan would throw problems like, “A Porsche 944 goes 0-60 in 8 seconds. If it weighs 3000 lbs. with fuel and driver, and half the engine power goes toward acceleration, how much power does the engine produce?”
Since then I’ve been a slide rule fan. I use one when flying for computing fuel burn rates, density altitude, altimeter & airspeed corrections. I also keep one around for doing random calculations that come up during the course of a day. When 2-3 sig figs of accuracy is sufficient, it’s quicker & easier than a calculator.
Slide rules are antiquated tech. So why learn to use them? It’s for these secondary benefits mentioned above. And they are fun.
Introduction
Slide rules are based on the concept of a logarithm (aka log). Every log has a base, and the log is what power you raise that base to get some other number N. Examples:
- Log base 10 of 100 is 2, because you raise 10 to the power 2 to get 100, or 10^2 = 100
- Log base 2 of 32 is 5, since 2^5 = 32
- Log base 10 of 42 is 1.623 (approximately), or 10^1.623 = 42
The reason logs are useful, and how they led to the invention of slide rules, is because exponents are additive. That is: 10^5 = 10^(2+3) = 10^2 * 10^3
That means if I know the logs of 2 numbers A and B, call them La and Lb, then La + Lb is the log of the product A*B.
Note: Computer scientists take advantage of this when multiplying many tiny numbers together. Since computer floating points have finite precision, multiplying many tiny numbers leads to underflow. Instead, take each number's log and add them all up. Then at the end take the inverse log of that sum. This gives you the same product with much higher precision since it never underflows.
Now suppose I have 2 rulers with markings from 1 to 10. But instead of being spaced linear like a normal ruler, they are spaced logarithmically. If I line up 1 on the first ruler, with some number A on the second ruler, then the mark for some other number B on the first ruler will line up with the value of A*B on the second ruler.
A picture’s worth 1000 words, so here’s a circular slide rule.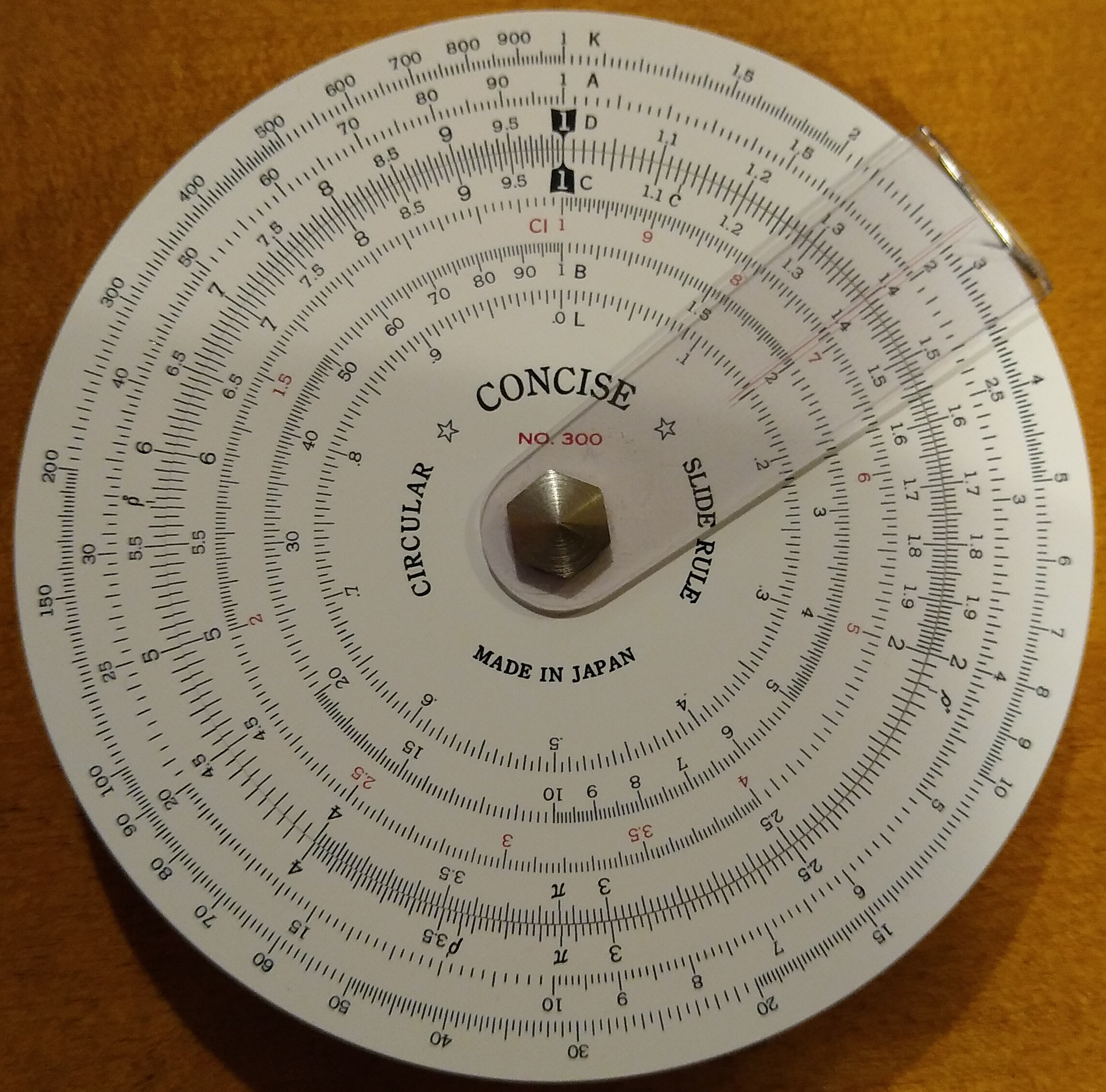
The clear marker with the thin red line is called the cursor. We’ll ignore that for now. See how the two black highlighted “1” values are aligned? Each of those scales (inner and outer) are logarithmic. That’s why the range from 1-2 takes about 1/3 of the scale while the range at the upper end is much more compressed. As you start from 1 and go up the scale, the numbers start out spread apart and get more squished together.
Watch what happens when we slide the inner “1” to line up with the outer “2”:
If this were a linear ruler, it would be shifted by 1 over the entire scale: 1 to 2, 2 to 3, 3 to 4, etc. But not here, where 1 matches 2, 2 matches 4, 3 matches 6, 4 matches 8, etc. Every number on the inner scale matches the number exactly twice as much on the outer scale. And every number on the outer scale matches the number exactly half as much on the inner scale.
Below I’ve highlighted what I’m talking about. Each number on the inner scale matches to exactly twice its value on the outer scale.
In short, this slide rule is set up to multiply or divide any number by 2.
Yet here’s the kicker: this is not specific to the value 2. It’s downright magical. Here’s the slide rule with 1 matched to 3:

Similar scenario, only now we can multiply or divide any number by 3. And look below for 4:

Of course, this doesn’t just work for integers. You can do this for any number in the scale. In fact, now you know how to multiply or divide using a slide rule.
BTW, these are called the C and D scales. On this slide rule, D is the outer and C is the inner. That’s what the C and D are in photos.
What about Zeros and Decimals?
Suppose you want to multiply 3*4. First line up the C scale 1 with the D scale 3, then look at the C scale 4, which points to the D scale 12. See the picture below:
You might notice that it doesn’t actually say 12, it says 1.2. We happen to know that 3*4 is 12, so we interpret the 1.2 as 12. When you use a slide rule you need to keep track of the decimal point.
This is where circular slide rules are easier to use than straight ones. On a straight rule, this 3*4 problem is greater than 1, so it goes off scale and you can't read the answer. You need to shift to additional scales CF or DF (C folded and D folded) to read the results. Circular slide rules never go off scale, they just wrap around. Much simpler and easier!
All Those Scales!
So far we’ve only covered the C and D scales. You can see that slide rules have several other scales. Most slide rules have these scales:
- C & D: multiplication & division
- CI: inverses
- A & B: squares & square roots
Some slide rules also have these scales:
- K: cubes & cube roots
- S, T, ST: sine & tangent
Let’s go through these one at a time.
CI Scale: Inverses
The CI scale is the inverse of the C scale and it’s marked in red. Simply put, it is the same scale but going backward – in the opposite direction. The C scale increases clockwise; the CI scale increases counter-clockwise. Each number on the C scale, lines up with its inverse on the CI scale. For example, 2 lines up with 5 since the inverse of 2 is 0.5.
Here, the cursor comes in handy to read these scales. For example, below the cursor is lined up on 4, so you can precisely read its inverse on the CI scale, which is 0.25. But as you can see all around the dial, each number on C always lines up with its inverse on CI, and both scales increase in opposite directions around the circle. I’ve marked some obvious points, like 4 and .25, 5 and .2, and their inverses.

For example, reading for yourself you can see that 1/7 is about 1.43. My calculator says it’s 1.42857. So we got 3 significant figures of accuracy there (more on sig figs later).
Conclusion
Now that you can use a slide rule for basic computations, have some fun practicing. I cover some of the other scales in part 2.

