It’s commonly said that digital audio’s resolution depends on the bit depth of each sample. Each bit doubles the range of amplitudes that can be stored, and a doubling of voltage is about 6 dB, so 16-bit audio is said to have 16 * 6 = 96 dB of resolution.
However, I believe that resolution is the wrong word. Here I will show that digital audio actually has virtually* infinite resolution at any bit depth. But first, let’s explore the common belief with an example.
Use REW to generate a single-tone sin wave, say 622 Hz at -114 dB. It sounds like this:
Of course you probably can’t hear it because -114 dB is very quiet. So let’s amplify it by +113 dB:
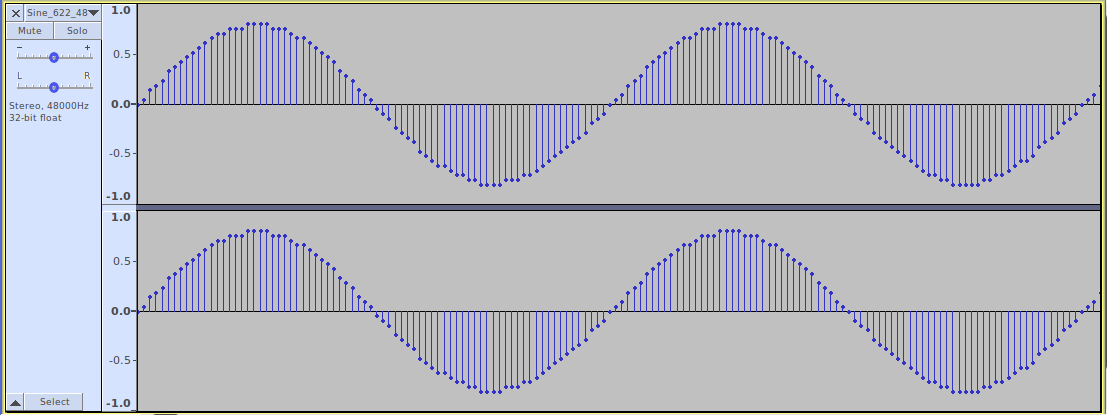
OK, that’s it. Yet experienced listeners may notice this doesn’t sound like a pure tone. It sounds a bit dirty. Let’s take a look at it:
You can see that the curve isn’t smooth. It has jagged jumps. This is called quantization distortion. We’ll get to this later. But the point is, the wave is there.
Now that we know this wave really exists, let’s take it at its original level of -114 dB and convert it to 16-bit. Here’s what that sounds like:
Nothing to hear, folks. It pure digital zeroes. No matter how high you turn it up, the only noise you’ll hear is from your sound card or amp.
Intuitively this makes sense. This wave’s peaks are too small; they never get anywhere near as loud as -96 dB, which is the smallest signal that 16-bit audio can capture. In fact, their peaks are a full 18 dB below that minimum threshold.
So, doesn’t this prove that 16-bit audio has only 96 dB of resolution? That is, it can’t capture anything below -96 dB? It seems so, but no — it doesn’t.
The reason for this is because I did the above transformations without using dither. But dither is an essential part of digital audio. When dithered, digital audio can capture signals well below -96 dB.
Here’s that -114 dB signal converted to 16-bit, with dither:
If that is too quiet to hear, here’s the same signal boosted by +90 dB (this is loud, so turn down the volume before playing):
That noise like tape hiss is the dither. You can clearly hear the sin wave in the noise. For comparison, here’s the above non-dithered transformation, boosted to the same level with dither:
This is pure noise/hiss without any signal. Comparing it to the above, the difference is obvious.
Conclusion
Here we’ve captured a -114 dB signal with 16-bit audio, which supposedly has only 96 dB of resolution. That’s 18 dB below its supposed minimum. Yet there’s nothing special about 18 dB. If it can go 18 dB below, there’s no arbitrary limit how much lower it can go. Eventually it will get masked by the noise so you won’t hear it anymore, but that happen far below 16-bit’s oft-quoted “resolution”.
This might seem like a contradiction, but it’s not. That’s because resolution is the wrong way to think about bit depth, leading to wrong notions about what actually is limited by bit depth.
Dither is what makes this possible, so it’s an essential part of digital audio. It enables us to capture signals well below the 6 dB / bit levels that are often quoted. Dither is not about psychoacoustics, it is about physics (or math, if you prefer).
What exactly is dither? Essentially, it’s randomizing the LSB (least significant bit) of each sample. Yes “random” means noise, so this adds noise to the signal. The irony is, adding noise increases the resolution. How much noise you get by randomizing the LSB depends on how “small” the LSB is. That is, it depends on the bit depth. With 16-bit audio, the LSB is -90 to -96 dB. With 24-bit audio, the LSB is -138 to -144 dB. In this sense, higher bit depths are like better quality analog tape having less hiss (though of course even 16-bit has far less noise than any analog tape ever invented).
Alternative Explanation
So how exactly does randomizing the LSB enable the samples to detect tiny signals below the bit depth? Here’s an intuitive way to think about this: every sample’s LSB is randomized, so 0 and 1 are equally likely. But when you add a tiny signal to this, it slightly biases the outcome. When the signal swings positive, the sum of signal + random LSB is slightly biased toward 1, meaning it’s slightly more likely to be 1 than 0. When the signal swings negative, the opposite happens.
Conclusion
In summary, digital audio can capture extremely low level signals well below its bit depth. The limiting factor for the smallest encodable signal is determined not by the bit depth, but by the noise level. At some point the dither noise will mask low level signals, but this happens well below the bit depth.