Digital audio requires an anti-aliasing filter to suppress high frequencies (at or above Nyquist, or half the sampling frequency). Without this, an infinite number of different analog waves could pass through the digital sampling points. With this, there is only 1 unique analog wave that passes through them. The anti-aliasing filter is essential to ensure the analog wave that the DAC constructs from the bits is the same one that was recorded and encoded (assuming that the original analog mic feed was properly anti-alias filtered, preventing frequencies above Nyquist from leaking through).

Note: what happens if the filter is not used at all?

• As I just mentioned, without a bandwidth limit, many different analog waves could be constructed from the same sampling points – which one is correct?
• Without a bandwidth limit, the DAC will produce an analog wave with frequencies above Nyquist, which must be distortion, since they could not be in the analog wave that was encoded.

Pragmatically, one might ask what is the problem, since the difference is all in frequencies above Nyquist, which we can’t hear? The problem is aliasing. Passing these high frequencies will cause the D-A conversion process to mis-interpret samples, creating an analog wave with spurious noise in the audible spectrum through a phenomena known as aliasing. So you get distortion in the audible spectrum – not just at supersonic frequencies. Intuitively, this effect is similar to watching a wheel spin in a movie; it sometimes appears to spin backward when it’s really spinning forward, because the frame rate (typically 24 / second) captures it at just the right moments. The wheel is spinning faster than “Nyquist” for 24 frames per second, which is aliased into the illusion of motion in the opposite direction happening slower than 24 frames per second.

So the DAC definitely needs a low pass filter to suppress frequencies above Nyquist. The question is – what kind of filter?

Audiophiles debate about whether linear or minimum phase anti-aliasing filters are ideal for sound reproduction and perception. Linear phase has the lowest overall distortion, but its symmetric response around transients (a bit of ripple just before and after a transient pulse), often called the Gibbs effect, means there is a “pre-echo” or “pre-ring”. In the diagram below, the red line is the signal and the black wave is the analog wave constructed from it using a linear phase filter.

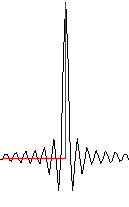If the X axis is t for time, this black curve is the function sinc(t). It is symmetric before and after the transient, which means it starts wiggling before the transient actually happens. This is unnatural; in the real world, all of the sound happens after the actual event. This pre-ringing is an artifact of linear phase anti-aliasing filters. Many audiophiles claim this is audible, smearing transients and adding “digital glare”.

Here’s what the audio books don’t always tell you. According to the Whittaker-Shannon interpolation formula, this sinc(t) response represents the “perfect” reconstruction of the bandwidth limited analog signal encoded by the sampling points. The pre-ring is very low level, and it rings at the Nyquist frequency (half the sampling frequency). That is at least 22,050 Hz (octaves higher if the digital signal is oversampled, as it virtually always is). This makes it unlikely for anyone to hear it even under ideal conditions of total silence followed by a sudden percussive SMACK.

NOTE: I say “unlikely” not “impossible” because even though humans can’t hear 22 kHz (let alone frequencies octaves higher), it is at least feasible that somebody could still hear the difference. Under the right conditions, removing frequencies we can’t hear as pure tones causes audible changes to the wave in the time domain. That doesn’t make sense mathematically, but human perception of the frequency & time domains is non-linear and not as symmetric as Fourier transforms.

Some audiophiles suggest minimum phase filters as an alternative to solve this problem. But this cure may be worse than the disease. Minimum phase filters have an asymmetric response around transients with no pre-ringing. A picture is worth 1,000 words, so here’s what that same impulse looks like when a minimum phase filter is used.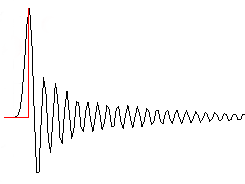

You can see that the impulse strikes instantly without any pre-ringing. Well it actually rings louder and longer than the linear phase filter, but that ringing happens after the transient.

This has the added benefit that the ringing is masked by the sound itself for the simple reason that loud sounds psychoacoustically mask quiet ones. So what’s not to like here?

The problem is, minimum phase filters actually have more distortion (more ringing, more phase shift) than linear phase. So you get more distortion overall, but it’s time-delayed so you get cleaner initial transients with more distorted decay. And the phase shift caused by minimum phase filters happens all the time, not just in transients. So it seems you can have clean transients, or good phase response, but not both. Choose your poison.

At this point a purist audiophile might hang his head in sadness. But there’s a better solution to the digital bogeyman of pre-ring: oversampling (or higher sampling rates). The phase distortion and ringing of any filter is related to its slope, or the width of its transition band. Oversampling further increases the frequency of the pre-ring (which was already ultrasonic), makes a shallower slope, wider transition band, reducing distortion.

For example consider CD, sampled at 44,100 Hz. Nyquist is 22,050 and some people can hear 20,000 so the transition band is from 20,000 to 22,050. That’s very narrow (only 0.14 octaves) and requires a steep filter with Gibbs effect pre-ring at 22,050 Hz. Oversample it 8x and Nyquist is now 176.4 kHz, so your transition band is now 20k to 176.4k, which is 3.14 octaves (actually, you’d use a lower cutoff frequency, but it’s still at least a good octave above 22,050 Hz). Absolutely inaudible; go ahead and use linear phase with no worries.

In short, use higher sampling frequencies (or oversample) not because you need to capture higher frequencies, but because it gives you a more gradual anti-aliasing filter which means faster transient response without any time or phase distortion.

This idea is nothing new. Most D-A converters already oversample, and have been doing so for decades. The pre-ring or ripple of a well-engineered DAC is negligibly small, supersonic and inaudible. However, some people prefer minimum phase filters! How can we explain that? Minimum phase filters have no pre-ripple, yet they also have phase distortion, they ring louder and longer, and in some cases they allow higher frequencies to be aliased into the signal.

First, if this preference comes from a non-blind test, we can’t be sure they really heard any difference at all. Maybe they did, maybe they didn’t. A negative result from a blind test doesn’t mean they can’t hear a difference, it only means we can’t be sure they hear a difference.

Along these lines of non-blind testing, Keith Howard wrote a good one for Stereophile a few years ago: https://www.stereophile.com/reference/106ringing
I love their experimental attitude: test and discover! But when they talk about how hard it was to tell the filters apart, it is kinda funny thinking about a bunch of middle-age guys wondering why they can’t hear a supersonic ripple well above the range of their hearing. Especially when most of them understand math & engineering well enough to know why.

Second, consider whether this preferences comes from a blind test. Blind tests only reveal whether people can hear differences; they don’t qualify exactly what differences they were hearing. Perhaps people who prefer minimum phase filters are simply finding some of these distortions to be euphonic. This seems reasonable, given that preferences for vinyl records and tube amps are also common. However, it could also be that some DAC chips implement one filter better than the other.

This topic has been endlessly debated in audiophile circles for years. Here’s an article showing some actual measurements: http://archimago.blogspot.com/2013/06/measurements-digital-filters-and.html

A couple years later he followed up with a listening test: http://archimago.blogspot.com/2015/04/internet-blind-test-linear-vs-minimum.html

So what do I think about all this? Like the Stereophile reviewers, listening to music, I find it difficult to hear a difference between the “sharp” (linear phase) and “slow” (minimum phase) filters. Test signals highlight the differences (I can hear the difference clearly with a square wave) but I don’t enjoy listening to test signals, and since they’re not natural sounds, even if you can tell them apart there’s no reference for what they should sound like. I know the sharp filter (when properly implemented) is correct from a math & engineering perspective, as long as it is properly implemented. The sharp filter in my DAC is only -6 dB at Nyquist, so it might not be properly implemented, though its slope is very steep at that point, so it’s probably not leaking supersonic noise which can be aliased into the audible spectrum. Since there’s essentially no audible difference, I prefer the sharp filter in my DAC. I made some measurements and this seems justified from a technical perspective.