Category Archives: Tech

Keyboard Switches: Summary

Tech
by Mike Clements

Introduction

Touch typing on mechanical switches is faster, more confident and satisfying than on bubble dome switches, because mechanical switches are more reliable and give tactile and audible feedback as you type. Yet all mechanical switches are not created equal. They have a wide range of attributes. I’ll discuss these attributes, name a few switches and list my favorites.

Switch Makers

Back in the day it was IBM with their buckling spring switches, the classic of the 1980s. Alps was another big switch maker. After IBM stopped making buckling springs Unicomp bought IBM’s patent and carried that torch forward to this day. Cherry entered the picture, then Gateron and Keychron. We also have smaller volume boutique switch makers like Zeal PC. And many others…

Some of these makers have shared the same color coding of their switches by attribute. More on this later.

Switch Attributes

Switches have 3 basic attributes:

  • Sound: how loud is the switch?
    • Ranges from silent to loud
  • Tactility: whether the switch has a tactile “bump” during the keypress
    • Ranges from linear (none) to highly tactile
  • Weight: how much force does it take to press the key?
    • Ranges from light (40 grams) to heavy (70+ grams)

Switches have additional attributes like smoothness, but the above 3 are the primary attributes by which they are grouped.

All high quality mechanical switches are reliable and durable, meaning no missed or double strikes (common with cheap bubble dome switches), and last for 50 M or more actuations.

The most common switch size & shape is Cherry. Gateron, Keychron, Zeal PC and others copy this design – it’s become the standard. The bottom of the switch has flat copper pins that stick straight down to connect to the keyboard backplane (whether press-fit or soldered). The keystem sticks up with a + shaped male connector, and keycaps have a center stem with a female connector that plugs in. The switch housing has top & bottom halves held together with press-fit snaps. They can be separated, disassembled and reassembled.

Switch Colors

Most of the common switches have colors that indicate their attributes, and these colors are mostly standardized across makers.

ColorSoundTactilityWeightNotes
BrownQuietLightVery Lightalmost linear, tactile barely perceptible
BlueLoudModerateLightfeedback more audible than tactile, high-pitch click
GreenLoudModerateModeratefeedback more audible than tactile, high-pitch click
BlackSilentNone/LinearModerate
YellowSilentNone/LinearLightmoderate linear: not too heavy nor too light
RedSilentNone/LinearVery Light
Buckling SpringLoudHighHeavyExcellent tactile feel, low-pitch clicky sound
ClickiezLoudHighModerateexcellent tactile feel, thocky sound, similar to a VT320 terminal
Zilent V2SilentLight/ModerateModeratesilent yet tactile

My Favorite Things

I like switches with plenty of feedback, both tactile and audible, with moderate to heavy actuation force.

My 2 favorite switches are Zeal PC Clickiez and Buckling Springs. I like them about equally, though the Clickiez are more convenient since they are Cherry compatible. However, these switches are both loud enough that I can’t type notes during Zoom calls, and they obstruct music on open-back headphones.

I don’t like silent switches, but the least bad I’ve tried are Zeal PC Zilent V2. They make several versions having different weights; I use 67 gram. Linear switches are the most common choice for silent switches, but lacking any feedback, they are not as satisfying or confidence inspiring. The Zilent V2 gives decent tactile feedback and is just as silent as linear switches. They feel like what Cherry Browns strive for, yet utterly fail to become. If Brown switches became smoother, more tactile, and didn’t suck anymore, they would become Zilent V2.

Lubrication

The latest fad is to lubricate switches. More specifically, lubricate the interface between the switch stem and housing, and the top & bottom of spring where it connects to the stem and housing. It’s a tedious process, as you must acquire special greases or oils, open the switch housing, take apart the switch, use a tiny paintbrush to apply grease exactly where needed, not too much nor too little, and reassemble the switch. It can take 4 hours to lube the 80-100 switches of a normal keyboard.

I’ve tried this and I’m not a fan. My lube experiment was successful and the switches were quieter and smoother. But they also felt sluggish, ruining their feel. Perhaps lubing just the spring and not the keystems would be better. But the spring usually doesn’t contribute much sound. IMO, lubing makes mechanical switches sound and feel more like the cheap bubble domes that we are trying to get away from.

Padding

Switches can be padded in 2 ways: in the keystem, or in the keycap.

Keystem padding is a rubber insert fitted into the keystem (inside the switch) that protrudes just a bit on the top & bottom of the side rails. It damps the top & bottom, softening the sound & feel when the switch hits the top & bottom of the stroke. Keystem padding is applied by the switch maker inside the switch and usually cannot be added afterward.

Keycap padding is an o-ring fitted around the center stem of the keycap. It damps the bottom-out of the switch, which hits the o-ring before plastic meets plastic. Keycap padding can be added to almost any switch or keycap, though it can conflict with some stabilizers. Keycap padding is easy to apply and to remove, and a set of o-rings only costs about $10, so it’s an experiment worth trying. O-rings come in different hardness and thickness. I prefer 40A hardness which is soft. For thickness, 0.2 mm is “L” and 0.4 mm is “R”. Most of the time I go with “L” but which works best depends on the application.

Keyboard Review: Keychron V10 Alice

Tech
by Mike Clements

Introduction

Over 20 years ago during Octane Software I was working 80 hours per week and typing a lot. As a fast touch typist (90-100 wpm) I’ve always loved buckling spring keyboards. But the ergonomics of a standard keyboard were giving me issues. It forces the forearms to be parallel, which means bringing your elbows close together in front of you. This is fine for a few hours, but not so great 12 hours a day 6 days per week. At the time, I got a Kinesis ergo keyboard that was split, tented, and adjustable. I liked the ergos but hated the bubble dome switches.

With a split keyboard, your forearms aren’t parallel. You sit closer to the keyboard with your elbows at your sides, further apart, while your hands come close together, so your forearms + body make a triangle whose point is your hands in front of you. This is a more comfortable position.

Ergo Keyboards with Mechanical Switches

Ever since then I’ve wanted a keyboard that has that split ergo shape (similar to the Microsoft layout) but with mechanical switches. Tough luck! Especially if you want a particular type of key switch, not the ubiquitous yet sucky Cherry Browns, which are barely better than bubble domes (if I sound like a keyswitch snob, yes guilty as charged). This means hot-swappable switch sockets.

I’ve found a few ergo keyboard options but none were all that appealing. Most were weird, pricey, with limited switch options and not hot swappable.

  • Kinesys: Advantage360, Advantage2
  • Truly Ergonomic
  • Ergodox
  • Atreus
  • Esrille
  • Matias Ergo Pro
  • Maltron

Enter the KeyChron Alice!

The Alice layout came out a few years ago in the DIY keyboard market. It’s a split layout similar to the old Microsoft Ergo keyboards, yet smaller, typically a 60% to 80% size. Since I use all the function keys, scroll-lock, page, etc. 75-80% is the smallest layout I can use. It looked promising, but as a DIY only option, you’d spend at least $400 (probably more) building one.

Last year, Keychron released four versions of this Alice layout: model 8 and model 10, in variants Q and V. Their site does a crappy job of explaining the differences, so here they are:

  • Model 8: 65% size / 68 keys
  • Model 10: 75% size / 88 keys
  • Variant Q: metal backplate
  • Variant V: plastic backplate

I don’t care about metal backplates; plastic is fine as long as it has solid build quality. And the Q variant costs an extra $100. So I got the V-10 model, which costs $104. That’s a great price for a keyboard like this:

  • 75% Alice layout
  • Knob/button (upper left corner)
  • Hot-swappable mechanical switches
  • Fully programmable via VIA & QMK
  • 4 layers (2 for Mac, 2 for Windows)
  • Programmable RGB lighting: color, brightness, pattern
  • Doubleshot PBT keycaps
  • Solid construction with high build quality
  • 3 switch choices: blue, brown, red

Reference: https://www.keychron.com/products/keychron-v10-alice-layout-qmk-custom-mechanical-keyboard

What’s not to like?

Setup

My setup includes:

  • Linux (Ubuntu 20) desktop
  • Windows 10 desktop
  • Windows 10 laptop
  • IOGear GCS1102 and GCS1104 KVM switches

Good Stuff

The keyboard had free shipping from China via DHL in less than a week. My first impression is quality and completeness. It’s fully disassemble-able and repair-able and comes with tools needed to take it apart. Build quality is excellent with high quality materials from the keycaps to stabilizers, case and construction. This appears to be a “lifetime” keyboard.

The first thing I did was set up the keys:

  • Removed the keycaps
  • Removed the switches (Keychron Blue)
  • Installed Clickiez switches (my favorite)
  • Installed o-rings on the keycap stems (0.2mm 40A)
  • Put it all back together

As I started typing, I sat closer to the keyboard with my arms in a more natural position and memories came back. After a few mins I pulled up an online typing test: 2 minutes averaging 92 WPM at 99% accuracy. This is close to my typing on normal keyboards. So the layout is quick and easy to adapt from a standard keyboard.

The keyboard has a small external switch next to where the cord connects that selects Mac vs. Windows/Linux mode. What it really does is set the default layer to 0 (Mac) or 2 (Windows). Layers 1 and 3 are accessed by using the Fn key from layer 0 or 2 respectively.

Bad Stuff

The Keychron mechanical switches (mine had Blue) are an imitation of Cherry or Gateron. They feel and sound about the same, but when I was pulling keycaps, two of them came up with the blue switch stem still attached, ripped it out of the switch body, which also broke off one of tabs (surprisingly tiny & delicate) that hold the switch stem inside the switch case. Take care when pulling keycaps from Keychron switches.

Note: Keychron support sent me 5 new blue switches. No hassles, no charge. Good support!

On a normal keyboard you can hit the “6” key with either hand (as I learned to type, the right hand is correct). Split keyboards give you no option. The Alice places the “6” key for the left hand only, which is just wrong. It will take me time to adapt to this.

The keyboard has 2 “B” keys, one for each side L and R. The proper use of B is with the L hand; I’ll never use the R side B key.

There is no R ctrl key. I use the ctrl keys on both sides without even looking, as it’s the most efficient way to activate various hotkey combos – just like the Shift key, ctrl-D using R ctrl, ctrl-P using L ctrl without lifting your fingers from the home position.

The cord plug-in point is exposed and has no strain relief. It would be better to recess it underneath the keyboard and provide molded recesses for cable strain relief, like most other keyboards do.

Through my KVM switch, this keyboard doesn’t support all its features. The knob doesn’t work, nor do the multimedia keys. And if you enable NKRO mode (Fn + N), it doesn’t work at all with the KVM switch. So with a KVM switch you must use the default 6-KRO mode. BTW, this is not documented and I lost hours troubleshooting why the keyboard wasn’t working at all through the KVM switch. Reloading firmware, etc. until I realized it was activating NKRO that caused the problem. Note that with other keyboards, the multimedia keys and NKRO do work through my KVM switch, so this issue is specific to Keychron.

When CapsLock is on, the LED lights up underneath the key. But the keycap is opaque and large, so it’s hard to see. Also, it’s always white so if your LED lighting is set to white, you’ll never see it. My solution was to drill a small hole in the upper side of the keycap. Now I can see the light easily, and it doesn’t interfere with typing.

The keycaps are very high quality: thick PBT with nice colors and sharp graphics. They not all the same height, which limits the ability to move them around if you change the key assignments. They seem to have OSA profiles. It would be better to achieve the ergonomic contour with the keyboard backplane instead of keycap heights, making the keycaps the same height and fully interchangeable. Even so, key swapping flexibility would still be somewhat limited, since some of the keycaps have different non-standard sizes.

The standard layout is missing some important keys that do exist in standard 87-TKL layouts having the same number of keys:

  • PrintScreen, ScrollLock, Pause
  • End
  • R side CTRL
  • Windows menu (it has the Win key but not the Menu key)

This keyboard does have 5 macro keys along the L side, so you can assign these. But you’ll most likely want to change the position of the Del, Home, End, PgUp and PgDn keys since they aren’t laid out in a logical way.

Fixes

Here are the things I’ve done to address some of the above issues:

  • Disable NKRO – so it works with my KVM switch
  • Change R side ALT to CTRL – since I use it more often
  • Change R side B to ALT – since I’ll never use R side B and I need ALT on that side
  • Change the R side vertical run to Home, End, PgUp, PgDn – to make it coherent
  • Change Ins (above Backspace) to Del – since that is near where Del is on an 87-TKL and I don’t use the Ins key much at all
  • Set M1 – M3 to PrintScreen, ScrollLock, Pause respectively – since I use these keys
  • Set M4 to Insert, just to have this key if I need it
  • Set Fn-Win to the Menu key – so I have both Win and Menu
  • Set backlight to yellow-orange (any color but white), so the caps lock light is visible

Key Counts and Matching

This keyboard has 88 keys, so it’s similar to an 87-TKL layout. Yet having 1 extra key doesn’t really mean you get an extra key. With 2 spacebars and B keys, some keys are wasted. And others are missing, like End, PrtScr, etc. Yet it also has 5 extra keys M1-M5. The net effect is that it is equivalent to an 87-TKL. That is every key on a standard 87-TKL layout can be mapped to a key on the V10 Alice. But the layout is different of course, though you have total flexibility to map these keys anywhere you want.

Final Updates

I use this keyboard at work, where I spent a lot of time on Zoom calls. Clickiez switches are too loud for Zoom, so I replaced the switches with Zeal PC Zilent V2 (67 gram) so I can type notes while on calls. More on that here.

Conclusion

Here’s what mine looks like – you can see that I swapped some of the keycaps to indicate my key changes:

I like this keyboard. It’s high quality for a great price. The layout requires some adaptation, but it’s not too weird out of the box, and it’s flexible and customize-able. It’s comfortable to type on for hours. The incompatibilities with my KVM switch are disappointing, but the workaround is OK. Combined with the hot-swappable switches, repairability, open source firmware, and good factory support, this is a great keyboard.

However, after a month or so I still couldn’t get used to the layout. Not the alphanumeric keys, those were fine. But I underestimated how often I use arrow keys, PgUp/PgDn, etc. And how often I must use standard keyboards (at home, on my laptop when traveling). I could have gotten used to the Alice V10 layout if it were the only keyboard I used, but that was not the case. Fortunately, I found someone at work who wanted this keyboard. Even so, this is among the best ergo keyboards and worth a try for anyone looking for an ergo keyboard with mechanical switches.

Slide Rules: Trig

Math, Tech
by Mike Clements

Introduction and basics in Part 1. Squares, Cubes and roots in Part 2. Here we cover trigonometry: sine, cosine and tangent. Not all slide rules have these scales, but when they do they are usually labeled as follows:

  • S: sine
  • T: tangent
  • ST: sine & tangent

Notes on these scales:

Trig Scales

You don’t need both sine & cosine, since they are inverse every 1/4 circle or 90 degrees. That is, for any angle A in degrees, sin(A) = cos(90-A). That’s why slide rules don’t have a cosine scale – it’s not needed.

Knowing a few key values of sine enables one to quickly estimate many problems (like crosswinds when landing an airplane) in your head. No need for a slide rule, let alone a calculator.

  • sin(0) = 0
  • sin(30) = 0.5
  • sin(45) = 0.707
  • sin(90) = 1

For small angles, sine and tangent are almost the same. Thus many slide rules have an shared ST scale for both, for small angles – typically less than about 5*. Exactly how close are sine and tangent for small angles?

  • 2 sig figs: 15* – sin & tan differ by the 2nd sig fig
    • sin(15*) = 0.259
    • tan(15*) = 0.268
  • 3 sig figs: 2* – sin & tan differ by the 3rd sig fig
    • sin(3*) = 0.0523
    • tan(3*) = 0.0524

Slide Rules!

Math, Tech
by Mike Clements

Background

I learned to use slide rules in high school in the 1980s. My physics teacher was one of the most memorable teachers in my life, “Mr. Jordan”. He said that slide rules can be faster than a calculator, and they promote a better understanding of numbers, orders of magnitude, and significant figures. They are not as accurate as calculators, but real-world problems only need 2-3 significant figures. As such, anyone who used a slide rule instead of a calculator would get a bonus 10% on every test, and answers would be considered correct if they were within 1% of correct. I was one of the few who took him up on this offer.

He handed out small circular slide rules, saying they were easier to use than linear slide rules (which is true, since circular never goes off scale). I don’t remember exactly what model slide rule it was, but the closest I know of today is the Concise model 28N. It was either that, or something very similar.

Note: I now have a Concise model 300, which is their biggest and best. The C and D scales are 8 cm in diameter, which is a circumference of 8π which is 25.2 cm, or about 10″. This is the slide used used in the photos below.

All we needed for physics was multiplication and division, and squares & cubes. Jordan would throw problems like, “A Porsche 944 goes 0-60 in 8 seconds. If it weighs 3000 lbs. with fuel and driver, and half the engine power goes toward acceleration, how much power does the engine produce?”

Since then I’ve been a slide rule fan. I use one when flying for computing fuel burn rates, density altitude, altimeter & airspeed corrections. I also keep one around for doing random calculations that come up during the course of a day. When 2-3 sig figs of accuracy is sufficient, it’s quicker & easier than a calculator.

Slide rules are antiquated tech. So why learn to use them? It’s for these secondary benefits mentioned above. And they are fun.

Introduction

Slide rules are based on the concept of a logarithm (aka log). Every log has a base, and the log is what power you raise that base to get some other number N. Examples:

  • Log base 10 of 100 is 2, because you raise 10 to the power 2 to get 100, or 10^2 = 100
  • Log base 2 of 32 is 5, since 2^5 = 32
  • Log base 10 of 42 is 1.623 (approximately), or 10^1.623 = 42

The reason logs are useful, and how they led to the invention of slide rules, is because exponents are additive. That is: 10^5 = 10^(2+3) = 10^2 * 10^3

That means if I know the logs of 2 numbers A and B, call them La and Lb, then La + Lb is the log of the product A*B.

Note: Computer scientists take advantage of this when multiplying many tiny numbers together. Since computer floating points have finite precision, multiplying many tiny numbers leads to underflow. Instead, take each number's log and add them all up. Then at the end take the inverse log of that sum. This gives you the same product with much higher precision since it never underflows.

Now suppose I have 2 rulers with markings from 1 to 10. But instead of being spaced linear like a normal ruler, they are spaced logarithmically. If I line up 1 on the first ruler, with some number A on the second ruler, then the mark for some other number B on the first ruler will line up with the value of A*B on the second ruler.

A picture’s worth 1000 words, so here’s a circular slide rule.

The clear marker with the thin red line is called the cursor. We’ll ignore that for now. See how the two black highlighted “1” values are aligned? Each of those scales (inner and outer) are logarithmic. That’s why the range from 1-2 takes about 1/3 of the scale while the range at the upper end is much more compressed. As you start from 1 and go up the scale, the numbers start out spread apart and get more squished together.

Watch what happens when we slide the inner “1” to line up with the outer “2”:

If this were a linear ruler, it would be shifted by 1 over the entire scale: 1 to 2, 2 to 3, 3 to 4, etc. But not here, where 1 matches 2, 2 matches 4, 3 matches 6, 4 matches 8, etc. Every number on the inner scale matches the number exactly twice as much on the outer scale. And every number on the outer scale matches the number exactly half as much on the inner scale.

Below I’ve highlighted what I’m talking about. Each number on the inner scale matches to exactly twice its value on the outer scale.

In short, this slide rule is set up to multiply or divide any number by 2.

Yet here’s the kicker: this is not specific to the value 2. It’s downright magical. Here’s the slide rule with 1 matched to 3:

Similar scenario, only now we can multiply or divide any number by 3. And look below for 4:

Of course, this doesn’t just work for integers. You can do this for any number in the scale. In fact, now you know how to multiply or divide using a slide rule.

BTW, these are called the C and D scales. On this slide rule, D is the outer and C is the inner. That’s what the C and D are in photos.

What about Zeros and Decimals?

Suppose you want to multiply 3*4. First line up the C scale 1 with the D scale 3, then look at the C scale 4, which points to the D scale 12. See the picture below:

You might notice that it doesn’t actually say 12, it says 1.2. We happen to know that 3*4 is 12, so we interpret the 1.2 as 12. When you use a slide rule you need to keep track of the decimal point.

This is where circular slide rules are easier to use than straight ones. On a straight rule, this 3*4 problem is greater than 1, so it goes off scale and you can't read the answer. You need to shift to additional scales CF or DF (C folded and D folded) to read the results. Circular slide rules never go off scale, they just wrap around. Much simpler and easier!

All Those Scales!

So far we’ve only covered the C and D scales. You can see that slide rules have several other scales. Most slide rules have these scales:

  • C & D: multiplication & division
  • CI: inverses
  • A & B: squares & square roots

Some slide rules also have these scales:

  • K: cubes & cube roots
  • S, T, ST: sine & tangent

Let’s go through these one at a time.

CI Scale: Inverses

The CI scale is the inverse of the C scale and it’s marked in red. Simply put, it is the same scale but going backward – in the opposite direction. The C scale increases clockwise; the CI scale increases counter-clockwise. Each number on the C scale, lines up with its inverse on the CI scale. For example, 2 lines up with 5 since the inverse of 2 is 0.5.

Here, the cursor comes in handy to read these scales. For example, below the cursor is lined up on 4, so you can precisely read its inverse on the CI scale, which is 0.25. But as you can see all around the dial, each number on C always lines up with its inverse on CI, and both scales increase in opposite directions around the circle. I’ve marked some obvious points, like 4 and .25, 5 and .2, and their inverses.

For example, reading for yourself you can see that 1/7 is about 1.43. My calculator says it’s 1.42857. So we got 3 significant figures of accuracy there (more on sig figs later).

Conclusion

Now that you can use a slide rule for basic computations, have some fun practicing. I cover some of the other scales in part 2.

Slide Rules: Past the Basics

Math, Tech
by Mike Clements

For background, here is part 1. It introduces slide rules and covers basic usage with C, D and CI scales. Here we cover the A, B and K scales for squares, square roots, cubes and cube roots.

A Scale: Squares and Square Roots

The A scale shows the square of each number on the D scale. Conversely, the D scale shows the square root of each number on the A scale.

Below the cursor shows that 3 on the D scale matches 9 on the A scale.

Note that as the D scale goes from 1 to 10, the A scale goes from 1 to 100. This means every single-digit number in the A scale has a corresponding double-digit number further up the scale. That is: 1 and 10, 2 and 20, 3 and 30, etc.

For example, below the cursor is on the A scale 30, showing the square root of 30 is 5.48:

So, squares are easy: just find the number on D scale and look to the corresponding number on A scale. But going the opposite direction, square roots, becomes ambiguous. What if you want the square root of a number that is not in the range of 1 to 100? For example:

  • If you want the square root of 400, on the A scale do you use 4 or 40?
  • If you want the square root of 4000,  on the A scale do you use 4 or 40?
  • If you want the square root of 0.5, on the A scale do you use 5 or 50?

First, observe that all of the single-digit numbers in the A scale occupy the first half, all the double-digit numbers the second half, and the split (the value 10) is exactly the mid-point of the scale. Thus, you can think of the A scale has having 2 halves. So the question boils down to knowing which half to use.

The answer is based on how many zeroes in the number whose root you want to know: is that number of zeroes odd or even? Adding or removing each zero (or each decimal point shift left or right) shifts back and forth between the 2 halves of the scale.

For example, consider the number 4.

  • The square root of 4 is 2 (low side of A scale).
  • The square root of 40 is 6.32 (high side of A scale).
  • The square root of 400 is 20 (low side of A scale).
  • The square root of 4000 is 63.2 (high side of A scale).

This pattern simply repeats. And it also repeats in the opposite direction:

  • The square root of 0.4 is 0.632 (high side of A scale).
  • The square root of 0.04 is 0.2 (low side of A scale).
  • The square root of 0.004 is 0.0632 (high side of A scale).

K Scale: Cubes and Cube Roots

The K scale works like the A scale. To cube any number N, find N on the D scale and look at the corresponding number on the K scale.

For example, this shows that 2 cubed is 8 (it actually shows that 2 squared is 4, and cubed is 8):

Yet the K scale also has the value 80, whose cube root is 4.31:

And the K scale also has the value 800, whose cube root is 9.28:

So while the A scale splits into 2 equal parts (1-10 and 10-100), the K scale splits into 3 equal parts: 1-10, 10-100, and 100-1000. Each of these occupies exactly 1/3 of the scale:

As with the A scale, cubing numbers is simple. Find N on the D scale and the corresponding K scale is N cubed. Yet doing the opposite, taking the cube root, is a bit more complex. You need to know which 1/3 of the scale to use. The procedure is a simple extension of what we did for the A scale. Yet since the A scale had only 2 parts, we thought of it as flipping back and forth. With the K scale having 3 parts, instead of flipping, each shift of the decimal point rotates forward to the next, or back to the prior part of the scale.

For example, consider the number 8:

  • The cube root of 8 is 2 (part 1 of  K scale).
  • The cube root of 80 is 4.31 (part 2 of K scale).
  • The cube root of 800 is 9.28 (part 3 of K scale).
  • The cube root of 8000 is 20 (part 1 of K scale).

It repeats every 3rd shift of the decimal point. And it also applies in the reverse direction as numbers get smaller:

  • The cube root of 0.8 is 0.928 (part 3 of K scale).
  • The cube root of 0.08 is 0.431 (part 2 of K scale).
  • The cube root of 0.008 is 0.2 (part 1 of K scale).

Exponents and Roots other than 2 or 3

Most everyday problems, especially those involving basic physics, use squares or cubes. Powers other than 2 or 3 are uncommon. Yet we do occasionally encounter them and you can solve them with a slide rule. The trick is to know some basic math rules about adding exponents.

Suppose we some number N, say 3.5, and we want to know N to some power, say the 7th power. So how would we compute 3.5^7 with our slide rule?

First, we split the exponent into smaller parts involving squares and cubes:

3.5^7 = 3.5^(2+2+3)

Next we split this out:

 3.5^(2+2+3) = 3.5^2 * 3.5^2 * 3.5^3

Now we have split the problem into squares and cubes so we can compute it on our slide rule:

3.5^2 = 12.2
3.5^3 = 42.8
12.2 * 12.2 * 42.8 = 150 * 42.8 = 6,430

Checking this with a calculator, I get 6,433.9. The slide rule gave us 3 significant figures.

Note: you can apply this same method with roots by taking the exponents as fractions. That is, the square root of 2 is 2 to the 1/2 power, cube root of 2 is 2 so the 1/3 power, etc.

What About that B Scale?

The B scale is the same as the A scale, used for squares and square roots. But it corresponds with the C scale instead of the D scale. Using D-A is the same as C-B. The B scale isn’t essential, but it is sometimes useful. On the Concise model 300, the A scale is along the outer circumference and the B scale is further inside. This makes the A scale longer and more accurate.

To quantify, on this Concise model 300 the A scale has a diameter of 9.2 cm and B scale 5.9. The A scale is 9.2 / 5.9 = 1.56 times longer. That’s a significant difference!

Conclusion

With squares and cubes, the power of the slide rule increases and we can solve a wider variety of problems. The next step is trigonometry: sine, cosine, tangent. These come up frequently in simple physics and everyday problems. This is covered in part 3.

 

Sanity Check: 0-60 Times

Cars, Math, Tech
by Mike Clements

With electric cars, the classic performance metric of 0-60 time has gotten much faster, approaching the theoretical limits of available traction. Yet some cars show 0-60 times even faster than this, which seems impossible. Accelerating faster than available traction requires thrust that doesn’t depend on traction, like jet or rocket engines.

I suspect that the 0-60 times being quoted for some of these cars are not real, but just theoretical projections based on power to weight ratio. Here’s a way to sanity check them.

Braking is already traction limited. So when acceleration is also traction limited, the car should accelerate 0-60 in the same distance and time it takes to brake from 60-0. These might be slightly different, due to the car’s uneven front-rear weight distribution and different sized tires front and rear. But it’s still a good rough guide and sanity check.

Braking 60-0 is usually given as distance rather than time. But assuming constant acceleration (not exactly true but a decent approximation) it’s easy to convert. Remember our basic formulas:

v = a*t
d = 1/2 * a * t²

The best street legal tires have a maximum traction of about 1.1 G. You can get up to about 1.3 G with R compound racing tires, but most are not street legal and the ones that are, don’t last more than 1,000 miles.

Here’s how we compute this for 1.1 G with English units:

60 mph = 88 fps
1 G = 32 fps/s
v = a*t --> 88 = 32 * 1.1 * t --> t = 2.5 secs
d = 1/2 * a * t² --> d = 1/2 * 32 * 1.1 * 2.5² --> d = 110 feet

Braking from 60 to 0 at 1.1 G takes 2.5 seconds and 110 feet. If you look at the highest performance cars, this is about equal to their tested braking performance. So, that same car cannot accelerate 0-60 any faster than 2.5 seconds because no matter how much power it has, that is the limit of available traction.

Some cars claim to do 0-60 in 2 seconds flat. This is 1.375 G of acceleration and takes 88 feet of distance. It might be possible with R compound racing tires, but not with street tires. Any car that actually does this in the real world, must be able to brake 60-0 in 88 feet. If its 60-0 braking distance is longer than 88 feet, then it takes longer than 2 seconds to go 0-60.

Note: there’s rule of thumb for cars whose 0-60 time is power limited (not traction limited). Divide weight in lbs. by power in HP, then take half that number. For example, a 3,000 lb. car with 300 HP has a ratio of 10, and will do 0-60 in about 5 seconds. This of course is only a rough approximation, but it’s usually close; it works because acceleration depends on power to weight ratio.

Keyboards: Clickiez!

Tech
by Mike Clements

On a recent day at work my friend Joe dropped by with a new keyboard he built. “Try it out for a few hours” he said. It weighed half a ton and had an unusual layout, smaller than an 87-TKL 80% keyboard. I plugged in its standard USB cable and as soon as I hit a few keys my jaw hit the floor and a flood of nostalgia tickled my brain. I was back in the UC Davis computer lab in the 1980s on a VT-320 terminal connected to a PDP-11 running Unix. I had forgotten how much I loved those keyboards, even more than the buckling springs that my 4.77 MHz Leading Edge Model D, and most other PCs, had at the time.

Turns out Joe built that keyboard with Clickiez switches. They’re amazing!

They are rated at 40 grams actuation, but this is misleading because it’s not peak actuation force. I measured by stacking pennies on them and got 70-75 grams. This is the same as buckling springs or Cherry MX Greens, a bit heavier than normal clicky switches like Cherry or Gateron Blues. Clickiez makes a heavier version, but don’t bother. 40 grams sounds too light but it’s not really 40 grams and it’s perfect.

The sound is quite unique. Compared to Cherry or Gateron clicky switches, they’re quieter and lower pitched with more of a “thwock” than “click-tick”. The tactile feedback is far superior to anything made by Cherry or Gateron. Crisp, definite, solid and consistent. This is an unbeatable 1-2 punch. These are the best switches I’ve ever typed on.

These switches are compatible with Cherry and Gateron. Same physical dimensions, same pin-outs. You can get a hot-pluggable keyboard with Cherry or Gateron switches and swap them for Clickiez. However, each Clickiez switch top-case has a slightly different shape than Cherry or Gateron, which may conflict with some kinds of key stabilizers. I didn’t run into this, but beware.

Another unique aspect of these switches is they can be configured in 3 modes:

  • Clicky (default): medium force, crisp, tactile
  • Tactile: slightly heavier force, slightly quieter, less crisp, more tactile
  • Linear: lightest force, quietest, not clicky, not tactile

In addition, you can choose to lube them, or to use o-rings on the key-cap stems. Joe loaned me his leftover switches and I tried all combinations. I didn’t like the lube. Makes them just a tad lighter, quieter, softer and less crisp. It doesn’t seem like a big difference with a single switch, but when you do an entire keyboard, it’s huge – it completely transforms the feel. Some people might like it, especially if they’re used to laptop or bubble dome keyboards. The problem with lube is once applied, it’s virtually impossible to fully remove. So test it first! Key-cap o-rings make them a tad quieter with less harsh bottom-out and shorter stroke. No change in the weight or crispness. Tactile mode feels a bit wonky to me. I prefer the crispness of the default mode, and it’s plenty tactile.

NOTE: to reconfigure Clickiez switches you must pop open the switch case, remove & re-install the metal click-plate in a different position, then snap the switch case top back on. It helps to have 2.0x magnification, and before you reinstall the switch case top, gently bend the 4 snap prongs inward to ensure a snug fit.

I couldn’t resist – I had to have a keyboard with these switches! Joe recommended a DIY kit keyboard, but they were expensive. I love his custom-made half-ton keyboard with its thick slab of metal baseplate, but it’s not for me. For a daily driver I had to have something more conventional and budget-friendly. So I ordered a set of 90 Clickiez switches and bought a high quality hot-swappable 87-TKL layout keyboard with Gateron switches. Total cost for both was about $250. I pulled the Gaterons and installed the Clickiez in their default configuration.

Michelle had an old keyboard with Cherry Brown clone switches that was starting to die. I let Michelle try my new Clickiez keyboard. She loved it so I told her keep it, I’ll build another for myself. It also has the advantage of wired USB instead of wireless, which is simpler with superior response.

So I put in another order and built a second for work. I installed o-rings on the key-caps but it’s still a bit loud for typing on Zoom calls. As I type for extended periods of time, there’s no finger or hand fatigue. The o-rings help there, as they soften the bottom-out of the keys.

Note: I got a Keychron Alice layout keyboard for work, and added ZealPC V2 Zilent switches. These are a silent tactile switch, great for Zoom calls and not annoying your work neighbors. I use the Clickiez at home.

I still love buckling springs and use them at home. A while back I compared them to Cherry Blues: http://mclements.net/blogWP/index.php/2021/10/19/keyboards-cherry-blue-vs-buckling-springs

Compared to Clickiez, buckling springs are a smidge heavier in actuation and a lot louder with a very different timbre. The Clickiez are so different it’s hard to say which is better. Suffice to say Clickiez are the only switch that even comes close to buckling springs. Both are leagues ahead of anything from Cherry or Gateron. One advantage of hot-swap switch sockets is the modularity makes it a “forever” keyboard. If any switch ever fails, simply replace it. Can’t do that with buckling springs. Some have said the Clickiez are unique but not necessarily a daily driver kind of switch. I disagree and find them most excellent for all-day use.

References / links:

Clickiez switches: https://zealpc.net/products/clickiez
87-TKL Keyboard: https://mechanicalkeyboards.com/shop/index.php?l=product_detail&p=9270
Alice Keyboard: https://www.keychron.com/products/keychron-v10-alice-layout-qmk-custom-mechanical-keyboard

Corda COUNTry: All in One Audio

Audio, Tech
by Mike Clements

Summary

The Meier Audio Corda COUNTry is a unique little device:

  • Equalizer, headphone crossfeed, reverb and other audio functions implemented in DSP (Digital Signal Processing)
  • Inputs (digital only): USB, SPDIF coax and toslink
  • Digital outputs: SPDIF coax and toslink
  • D to A converter
  • Analog output: single ended RCA (line level, volume controlled)
  • Analog output: single ended 1/4″ headphone jack

Its purpose is to adjust or tailor the sound to listener preferences. You can use it in many ways, though they fall into 3 categories:

  1. Pure DSP upstream from your DAC
  2. Headphone amp
  3. Preamp

In the first case you already have a headphone amp or preamp and you only want the DSP features. In cases (2) and (3) the COUNTry is an all-in-one device. The COUNTry was originally designed for (1) without any D/A or analog outputs. Later, the D/A and analog outputs were added since they increase flexibility with minimal cost impact.

The COUNTry operates internally at a single fixed sample rate: either 96k or 192k (buyer’s option). Digital inputs are resampled (if necessary) to this rate. I received a 192k unit.

The COUNtry

As auditioned, tested, measured

Features

I’ll review the features in the order in which I might use them most myself. With some of the features, like crossfeed and reverb, I couldn’t imagine a way to measure them. However, I did use and listen to all the features, and found that each does what it says and the effect is easily audible.

Measurements

I measured the COUNTry using a PC running Ubuntu 18, an ESI Juli@ sound card, with Room EQ Wizard software. I also have an SMSL SU-6 DAC and a JDS Atom amp. The Juli@ SPDIF coax output went directly to the COUNTry. I measured it in 2 ways:

  • COUNTry analog line level outputs to Juli@ analog inputs
  • COUNTry digital SPDIF coax output to SMSL SU-6 DAC, to Juli@ analog inputs

This measured the COUNTry as an all-in-one device with D/A conversion and analog output, and also as a DSP-only device upstream from a separate DAC.

The Juli@ sound card is high quality, but it’s nothing like professional measurement equipment from manufacturers like Audio Precision. I can measure the basics (frequency response and distortion), but take the measurements that follow as directional guidance within the limitations of my equipment.

Equalizer

The equalizer’s 7 bands have equal octave spacing with frequency ratio of 2.5:1 or 1.32 octaves. They are symmetric and complementary, so they can be combined without ripple. A picture’s worth 1000 words, so here are frequency response graphs of the positive and negative ranges respectively, showing each control individually, and all combinations.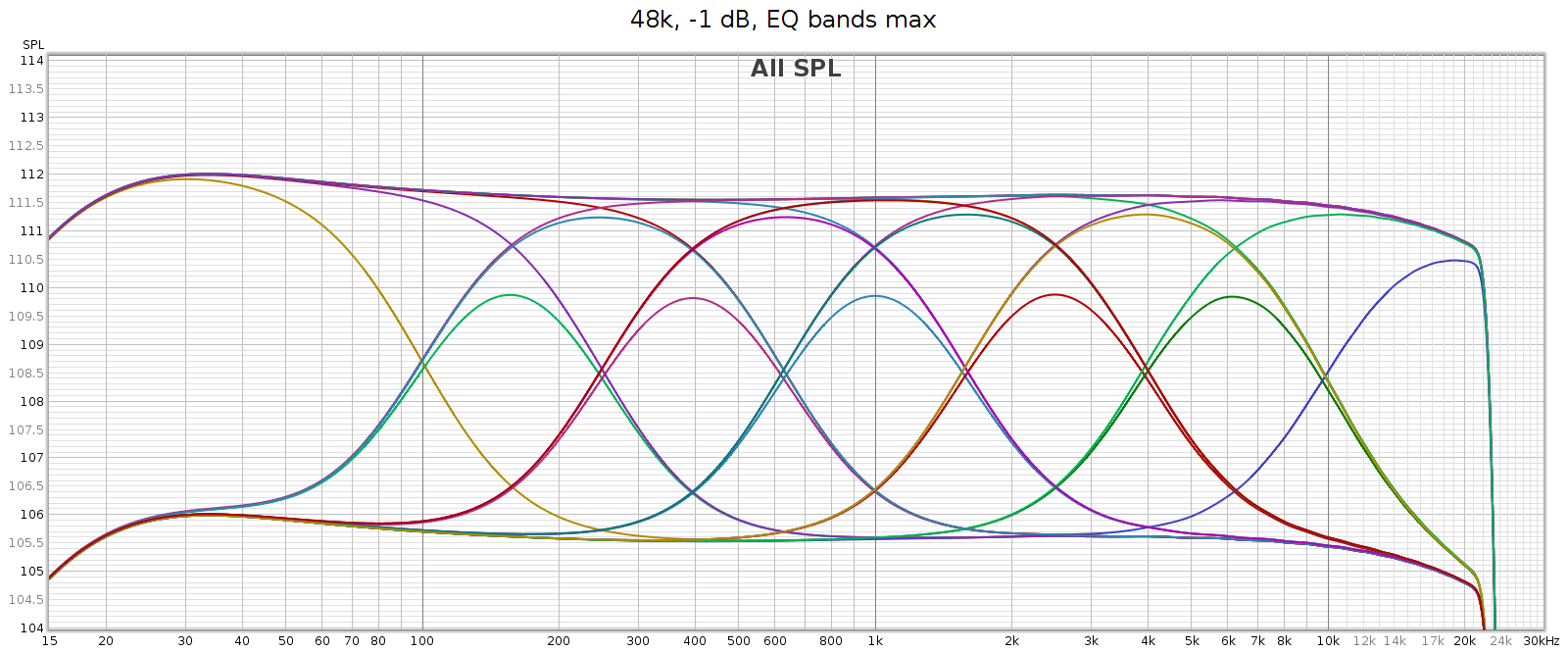

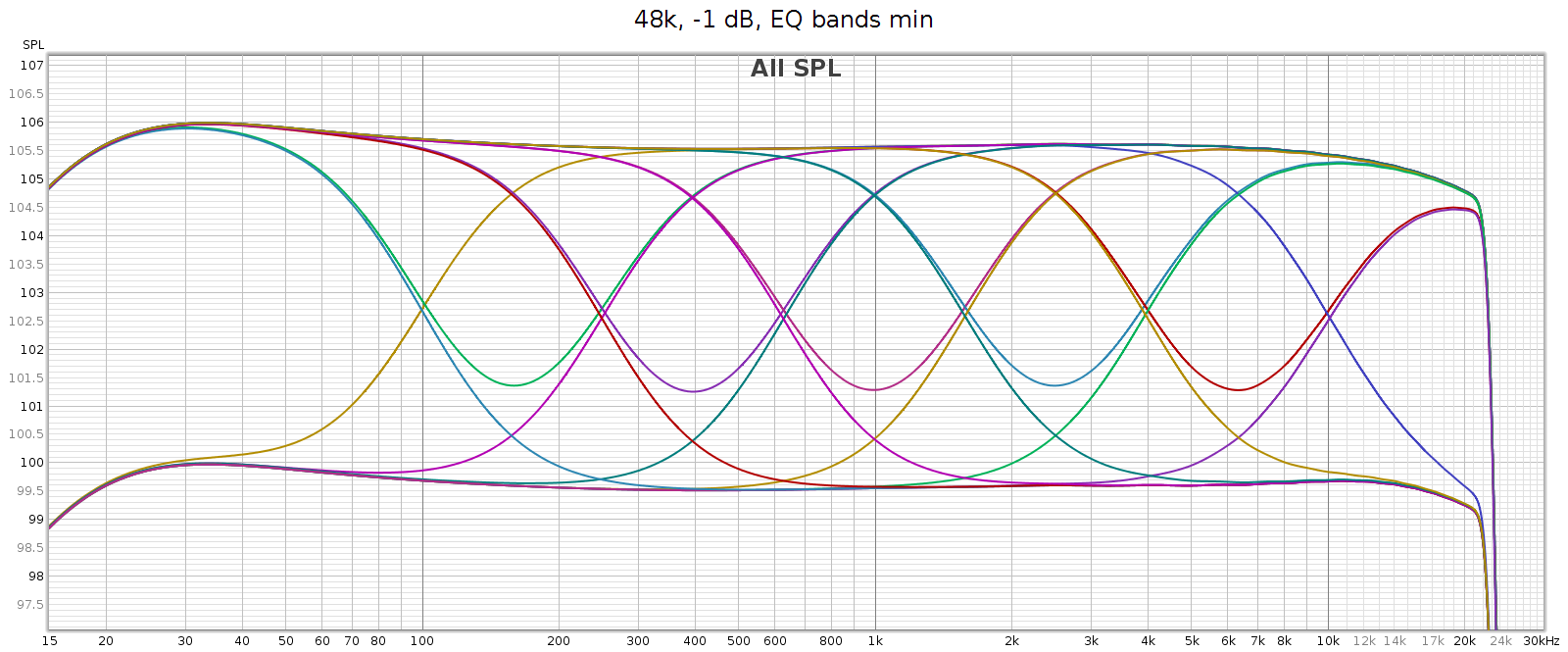
The manual says each band is +/- 6 dB, which is roughly true yet oversimplified. The max effect of any single band is +/- 4.3 dB. Two adjacent bands maxed together is +/- 5.7 dB. Three or more is 6.0 dB.

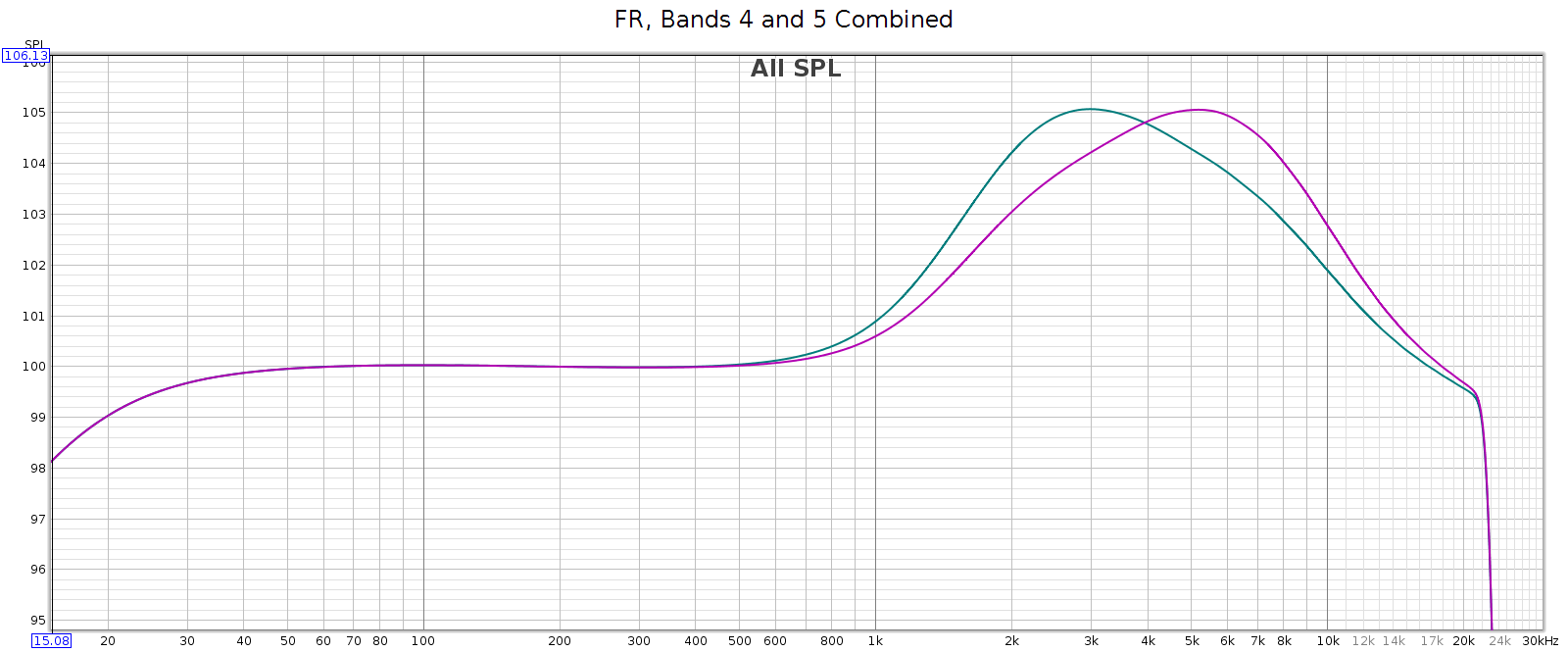
This enables adjacent sliders to be combined to form new bands. For example, consider sliders 5 and 6, centered at 2.5 and 6.2 kHz respectively. What I need to adjust the LCD-2F headphones is a slightly wider band centered at 4 kHz. And that’s exactly what I get when using both together, as you can see in the above frequency response graph. And, you can use different levels of these 2 sliders to shift the combined center frequency a bit higher or lower, to get a center frequency anywhere between 2.5 and 6.2 kHz. This makes the COUNTry’s EQ even more versatile than it appears.

For example, the following chart shows two combos: band 4 at max with band 5 at half (in teal), and band 4 at half with band 5 at max (in magenta). You can see the center frequencies are 3 kHz and 5 kHz respectively.

Regarding slider sensitivity: the following shows the center 1 kHz band at positions 1/4, 1/2, 1, 2, 3, 4, 5 and 6: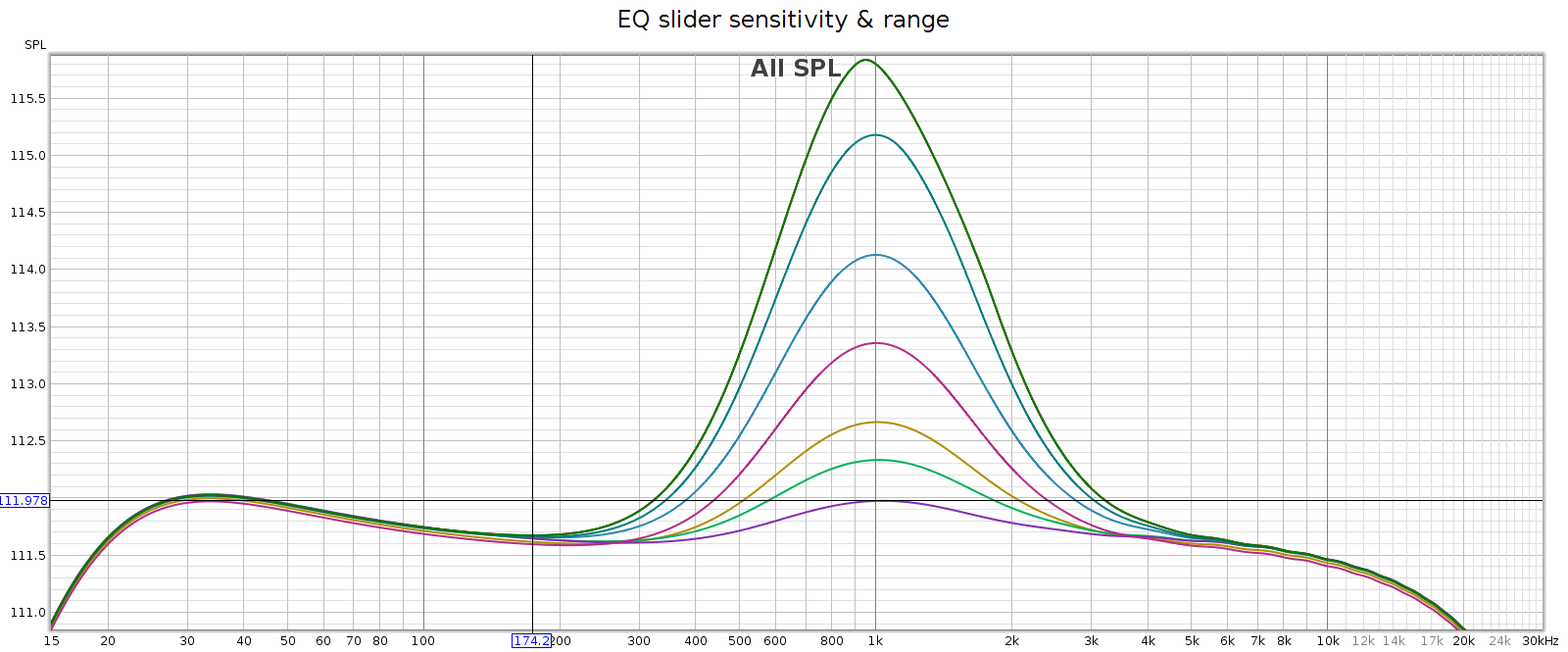

The slider effects are nearly continuous down to a fraction of a dB, allowing very small gradations. Each slider has 6 marked notches on each side (positive & negative), though only the center position is a tactile notch. The first 4 marks are about 1 dB each. The 5th mark is another 0.7 dB, and the 6th / last / max mark is the same as the 5th.

I like this design: it works like a conventional equalizer, but is more flexible. It’s a creative solution to an old problem.

Bass Boost

What: a gentle bass lift starting at 200 Hz and gradually increasing to + 6 dB at 20 Hz. This closely follows the bass attenuation of the popular Sennheiser HD-580 and HD-600 headphones, which is nice. It also mirrors the COUNTry’s bass attenuation in high gain mode, so use it if you want flat response in high gain. Its measured curve is shown twice in the following graph:

  • The top red line versus the green line.
  • The purple line versus the bottom orange line.

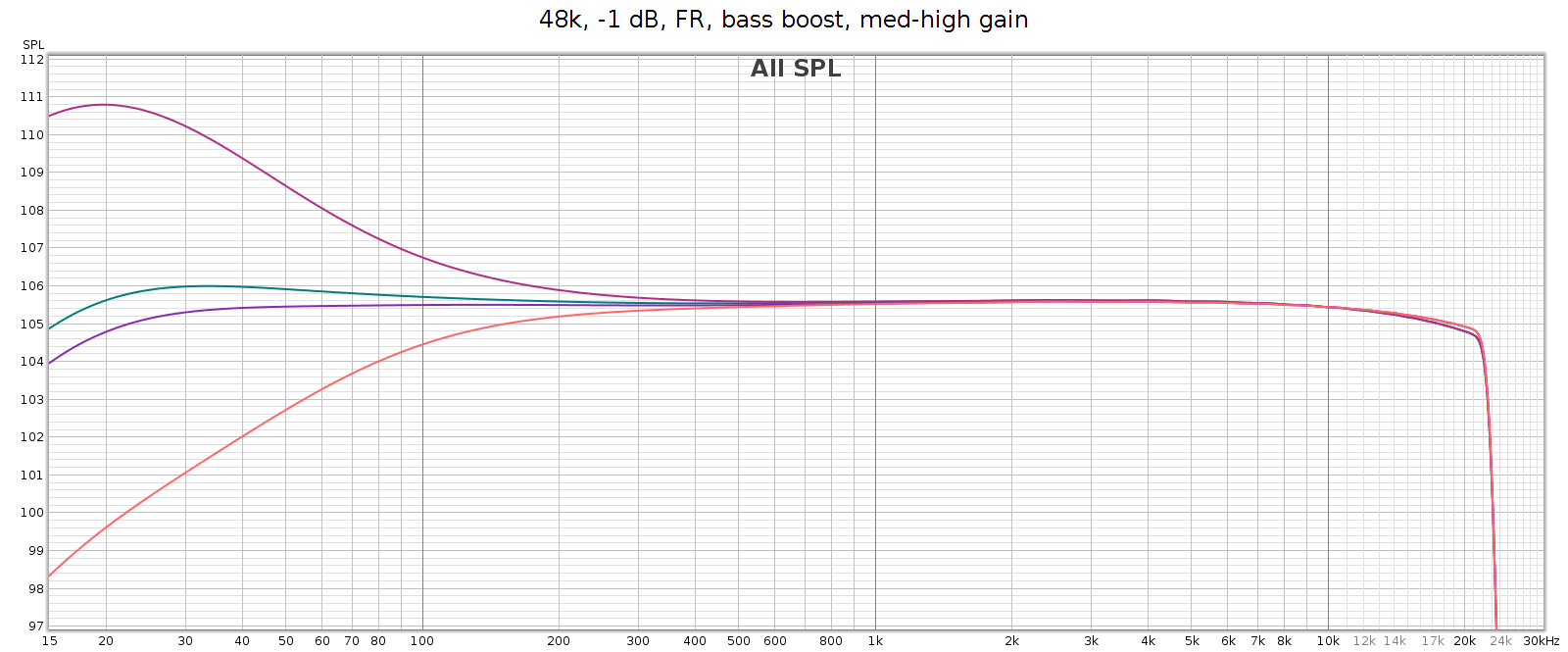
The manual says it’s a shelf boost with center frequency of 45 Hz and Q=0.5, which is true to the measured response. Q=0.5 is such a gentle slope that it is +1 dB as high as 120 Hz (evident in the above graph).

Stereo Crossfeed / Expander

Some recordings have sounds hard-panned to the left or right channels. This sounds wonky on headphones. Unfortunately, this was a common recording technique in jazz albums from the 1950s and 1960s – for example the classic Miles Davis / Coltrane album Kind of Blue. Crossfeed mixes a little of these sounds into the opposite channel, with a brief delay; it narrows the stereo separation. When listening to albums like this, it makes it sound more natural. The COUNTry has 7 levels of crossfeed (the Soul has only 5), and an 8th switch position that is mono (standard mono without crossfeed or delay). I don’t use crossfeed for normal listening, but it’s one of my favorite features because it’s so nice for those albums that need it.

Note: when clicking into mono, the sound suddenly becomes more dull. This effect is purely perceptual – the measured frequency response is exactly the same as in normal stereo.

Stereo expander does the opposite, making stereo wider. It’s intended for speakers but you can hear the effect somewhat on headphones.

Notch Filter

Many headphones have a resonance that causes a spike in frequency response in the 6k to 11k range. The COUNTry has a notch filter that cancels these spikes. Here’s the measured response of all 15 of the settings. It measures true to the specified Q=2.0, -6 dB.

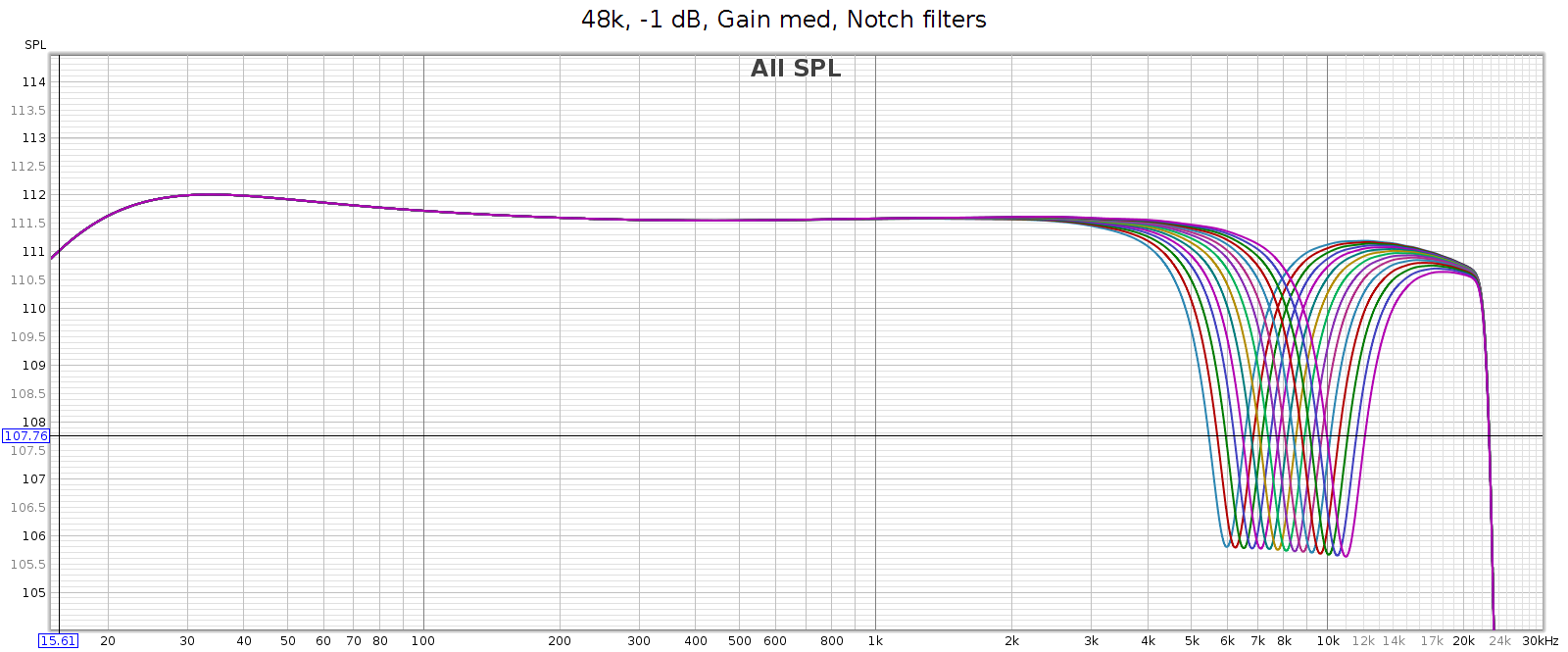
My Sennheiser HD-580 and Audeze LCD-2F don’t have such a spike, so I don’t use this feature. But the Sennheiser HD-800 does, as do many other popular headphones, making this a useful feature.

Reverb

This does exactly what it says: it adds reverb to the music. I’ve tried it with various recordings across a variety of musical styles from classical, to jazz, rock, etc. It’s not my cup of tea, as I prefer dry recordings. Yet this is a personal subjective thing. The reverb sounds natural and well implemented, and has 3 levels to play with.

Volume Control

The volume control feels analog but is digital, having perfect channel balance at every step from max to min. It also lights up an LED at certain exact positions: 0 (max), -6, -12, -18, and -24. This is useful for setting levels to avoid clipping when using DSP features.

Analog Gain

The COUNTry has 3 gain levels for its analog outputs: low, medium and high. Strangely, in high gain it attenuates low frequencies. The manual says this is to reduce excessive excursions of drivers at high levels. This doesn’t make sense to me, since high gain would be used for low sensitivity headphones or amps that need more voltage for the same sound level. And the COUNTry enables you to adjust the low frequencies if you want to. However, the bass boost switch exactly mirrors this bass attenuation, so if you are using high gain mode, turn on bass boost to get flat frequency response.

We’ve heard the mantra “the more gain, the more pain”. This is generally true, due to the constant gain * bandwidth of the transistors & opamps used in amplifiers. Because of this, the best approach is normally to use low gain whenever possible. That is, for a given loudness level, low gain at a higher volume position is usually cleaner than medium or high gain at a lower volume position. This also preserves digital resolution.

Note: This is especially true with conventional analog potentiometer volume knobs, which typically have better channel balance at high settings. However, the COUNTry's digital volume control has perfect balance at all settings. So that's not a factor here.

To test how the gain affects noise & distortion, I measured the COUNTry noise & distortion at each gain setting, with volume adjusted so that each had the same output level. Because the volume knob is digital, I couldn’t match the levels exactly, but I could match within 0.3 dB. More specifically:

  • Low gain at volume -6 dB
  • Medium gain at volume -16 dB
  • High gain at volume -26 dB

Medium gain measured slightly cleaner than high gain, but only slightly. Low gain was about the same as medium gain. So with the COUNTry, the gain level you use doesn’t make a significant difference in distortion or noise. Just select the gain that matches the sensitivity of the downstream device the COUNTry is driving. Of course, remember that high gain attenuates bass so use the bass boost to get flat response.

CD De-Emphasis

As mentioned above, the 7 band EQ has a creative design that eliminates ripple across the bands and enables adjacent bands to be combined to shift center frequencies. However, the highest band (16 kHz) has a special feature. When set to the minimum, it applies the Redbook CD de-emphasis curve. It’s nice to be able to apply this manually since some old CDs use it, they sound much too bright unless it’s applied, and many aren’t formatted properly for DACs to recognize and apply it automatically.

However, the equalizer slider has no indication when this triggers. It triggers at the bottom position, but as you raise the slider, it moves a short distance before disabling de-emphasis and attenuating the 16 kHz band. If you want the most 16 kHz attenuation without triggering de-emphasis, you must do it by ear. Slide it all the way to the bottom, then slowly lift it until the sound suddenly gets a bit brighter. It would be nice to have an indicator that lights up when de-emphasis is activated. The LED on the 16 kHz hand is already used as a power indicator, but it would be nice to have it change color or blink when de-emphasis is activated.

Miscellaneous

The measured impulse response is symmetric and phase response is flat into the high frequencies, which means the COUNTry uses standard linear phase filtering, rather than minimum phase.

The case and knobs are constructed in a manner that appears easy to disassemble and service. It’s good to see this exception to our modern age of cheap disposable equipment. I did not test this by opening the unit, since it is just a loaner.

Support is excellent. You can contact Jan Meier of Meier Audio directly on the company website or on Head-Fi. He is responsive, knowledgeable and helpful.

Usage and Build Quality

The COUNTry is a nice little device with an unusual look. It’s an “old-school” look and feel with physical knobs and LEDs instead of a display screen with menus. It has high build and parts quality.

Some of the indicators are a bit obscure but they become intuitive as you use them. For example, the digital sample rate display is done with 2 LEDs. One for the base rate (32, 44, 48) and another to indicate a multiplier (2x or 4x). Another LED lights up when the volume control is exactly at certain positions: 0 (max), -6 dB, -12 dB, -18 dB and -24 dB. This is a nice guide for setting precise levels.

The rotary switches make a solid “snap” and feel like professional test gear. The toggle switches are similar. The EQ sliders feel like potentiometers,  smooth with just the right amount of friction. The COUNTry is fully digital, so it detects the slider position and translates to a digital value. There is a tactile detent for the center position, but no others indicating when it’s shifted from one value to another. The controls feel good to use.

The headphone jack is seriously robust and overbuilt. The back panel connectors are not as robust but still feel solid. This makes sense as the headphone jack is likely to be plugged & unplugged much more often than the rear connectors.

Sound Quality (Subjective)

OK so what does it actually sound like? I listened on my Sennheiser HD-580 headphones. They are over 20 years old, but have fresh pads and I recently tested them with a MiniDSP EARS rig. They still have measured performance like new. I also used Audeze LCD-2F headphones (also tested & measured). The sound source was my PC with its ESI Juli@ sound card, and lossless FLAC files at bit rates ranging from 44.1 to 192. The Juli@ card coax SPDIF output routed to the COUNTry. I routed the COUNTry’s SPDIF digital output to my SMSL SU-6 DAC and JDS Atom headphone amp. With this setup, I could plug the headphones directly into the COUNTry, or into the JDS Atom. This enabled me to test the differences (if any) between the COUNTry in pure digital mode, versus its D/A and analog outputs.

I level matched by playing white noise, routing the analog outputs to my Juli@ card and measuring the level. With the JDS Atom’s analog volume knob, this enables level matching to about 0.1 dB.

In a word, the COUNTry sounds just a bit brighter than the SU-6 + JDS Atom. I first noticed this with music, and confirmed it with pink noise, which is a useful test signal for hearing subtle differences in frequency response. This brightness was unexpected, since the COUNTry’s analog frequency response has a slight bass boost and treble cut. However, the brightness sounds like it’s in the upper mids / lower treble, rather than in the highest frequencies. Loud parts with many instruments playing (like a symphonic crescendo) are slightly less resolved on the COUNTry analog output, compared to the SU-6 + JDS Atom.

Subjectively, the COUNTry analog output has a good clean sound across a variety of music with no obvious issues or artifacts. Though it’s not state of the art in terms of linearity, smoothness or detail – nor was it intended to be. Think of the COUNTry analog outputs as a sonically competent add-on feature. The COUNTry digital outputs are more transparent.

When you plug in headphones while the COUNTry is playing, it sometimes emits two loud CLICKs in the headphones, then pauses for about 1 second before the music starts. Inserting the headphone plug quickly usually avoids this. Meanwhile, the line level outputs are always playing and do not pause or CLICK. If you power on the COUNTry while it has musical input, you get a single loud CLICK then the sound starts playing in the headphones.

Anomalies

Frequency Response

Analog frequency response is not quite flat, and different in low (blue), medium (green) and high (red) gain. Medium gain has a 0.5 dB lift in low bass, and high gain has a 6 dB drop in low bass. All modes gently taper high frequencies, reaching about -0.6 dB at 20 kHz.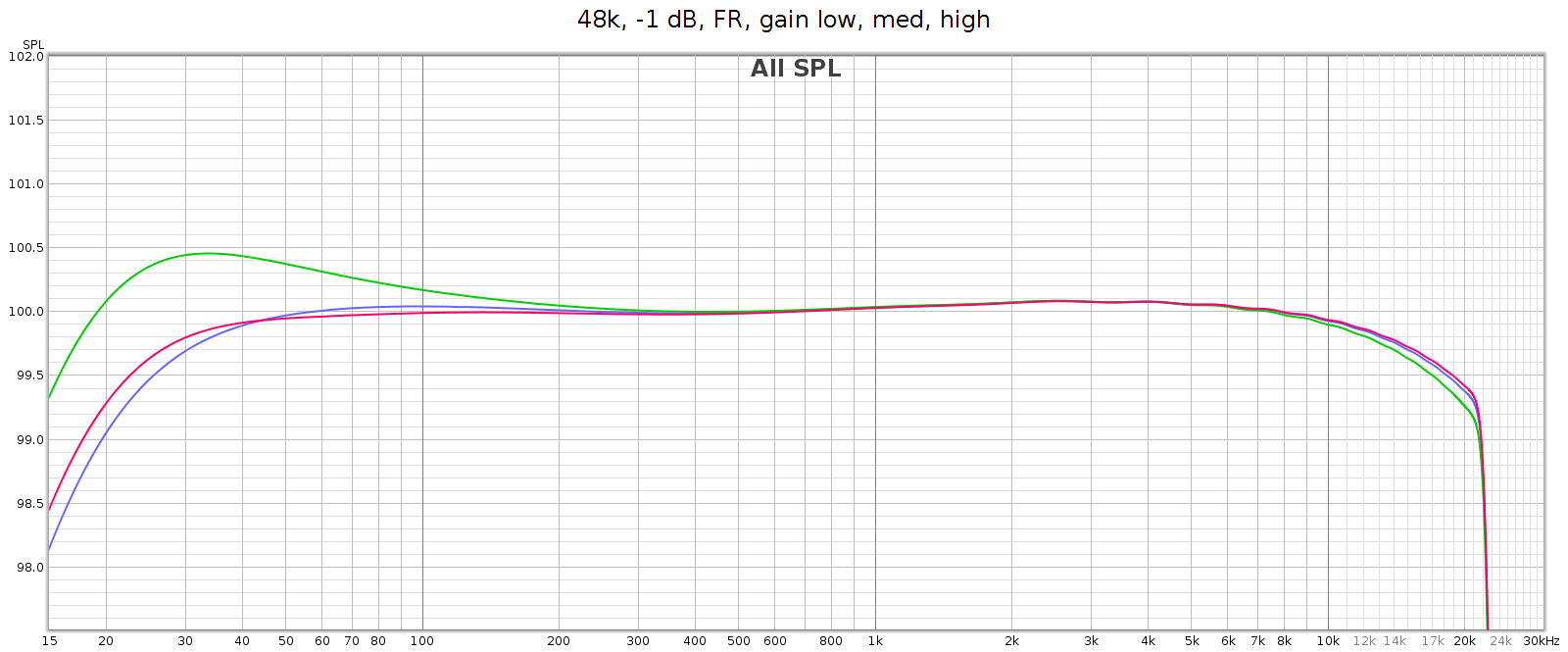

Note: in the above high gain curve (red), digital bass boost was applied to flatten the response. The uncorrected response is shown in another graph below.

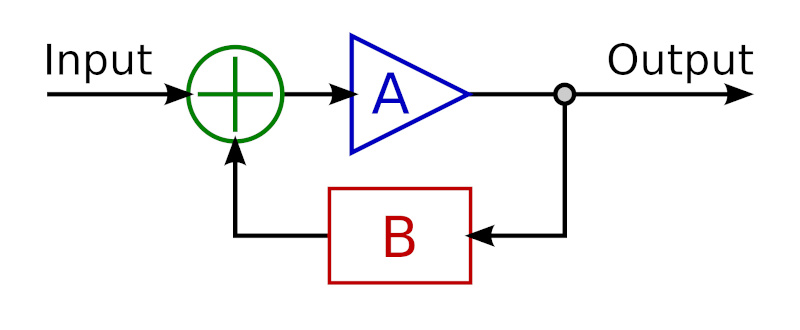
Why the frequency response differences at different analog gain levels? This is due to the Meier Audio FF or Frequency Adaptive Feedback. It attenuates low frequencies in the digital inputs, then boosts them back to flat again in the analog outputs. This means the attenuation curve (implemented in DSP) must match the boost curve (implemented in passive analog components). Meier Audio optimized this matching at low gain, since they expect that will be most often used. The purpose of FF is to frequency shape and optimize DA conversion and the gain-feedback loop, so it is only used for the analog outputs, not on the digital outputs.

As mentioned above, in high gain the frequency response attenuates bass beginning at 200 Hz, gradually reaching -6 dB at 20 Hz (this is noted in the manual). The COUNTry has a DSP bass boost that applies the exact reverse of this. So if you want flat response in high gain mode, turn that on (as it is in the above graph).

Let’s take another look at the bass boost frequency response graph shown earlier. From bottom to top:

  • Orange is high gain
  • Purple is high gain with bass boost activated
  • Green is medium gain
  • Red is medium gain with bass boost activated

The COUNTry’s digital output is smoother and more linear, but still has gentle HF attenuation reaching -0.6 dB at 20 kHz, and even gentler LF attenuation about -0.2 dB at 20 Hz. We see below that this slight attenuation happens in the digital domain. This graph shows the digital output with all sampling rates on top of each other:

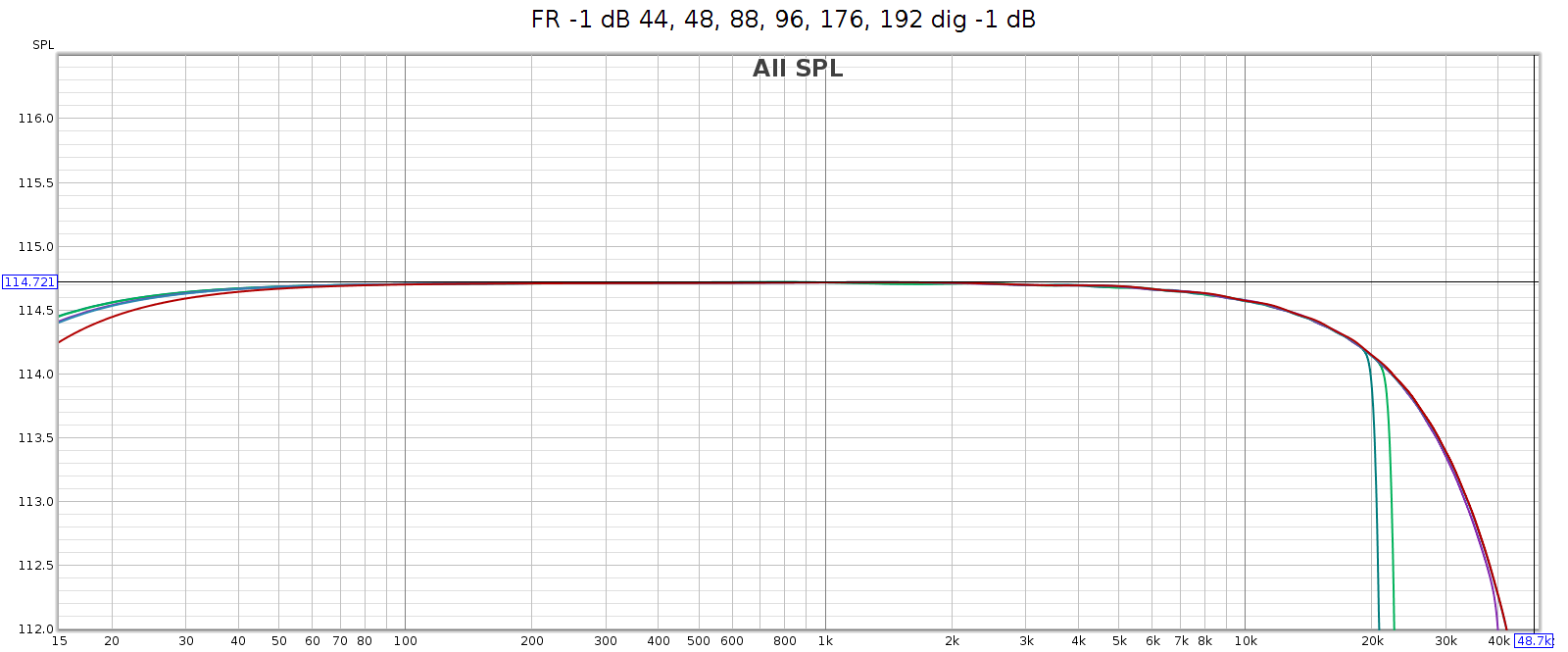
Noise at High Sample Rates

At high sample rates (176.4 and 192) the COUNTry has a lot of high frequency noise. This is unexpected and unusual, so I tested in several different ways:

  • Analog outputs
  • Analog outputs at lower levels (-6 dB, -12 dB)
  • Analog outputs with lower digital input levels (to -48 dB)
  • Analog outputs with input from my phone (USB Audio Player Pro) in bit perfect mode, instead of from my computer (ESI Juli@ sound card)
  • Digital outputs
  • Digital outputs at lower levels (to -48 dB)

It measured the same in all cases. This suggests the issue is not in the D/A conversion or analog stage, but in the DSP.

Here’s what that noise looks like at 176.4 kHz. Actually, in the graphs below it looks like distortion rather than noise, but more on that later. The horizontal line at y=0 dB is the sweep signal. It is not really at 0 dB, but this is relative to facilitate reading the levels. The brown line is noise. The black line is THD. The colored lines are 2H, 3H, etc., which sum to the black line.

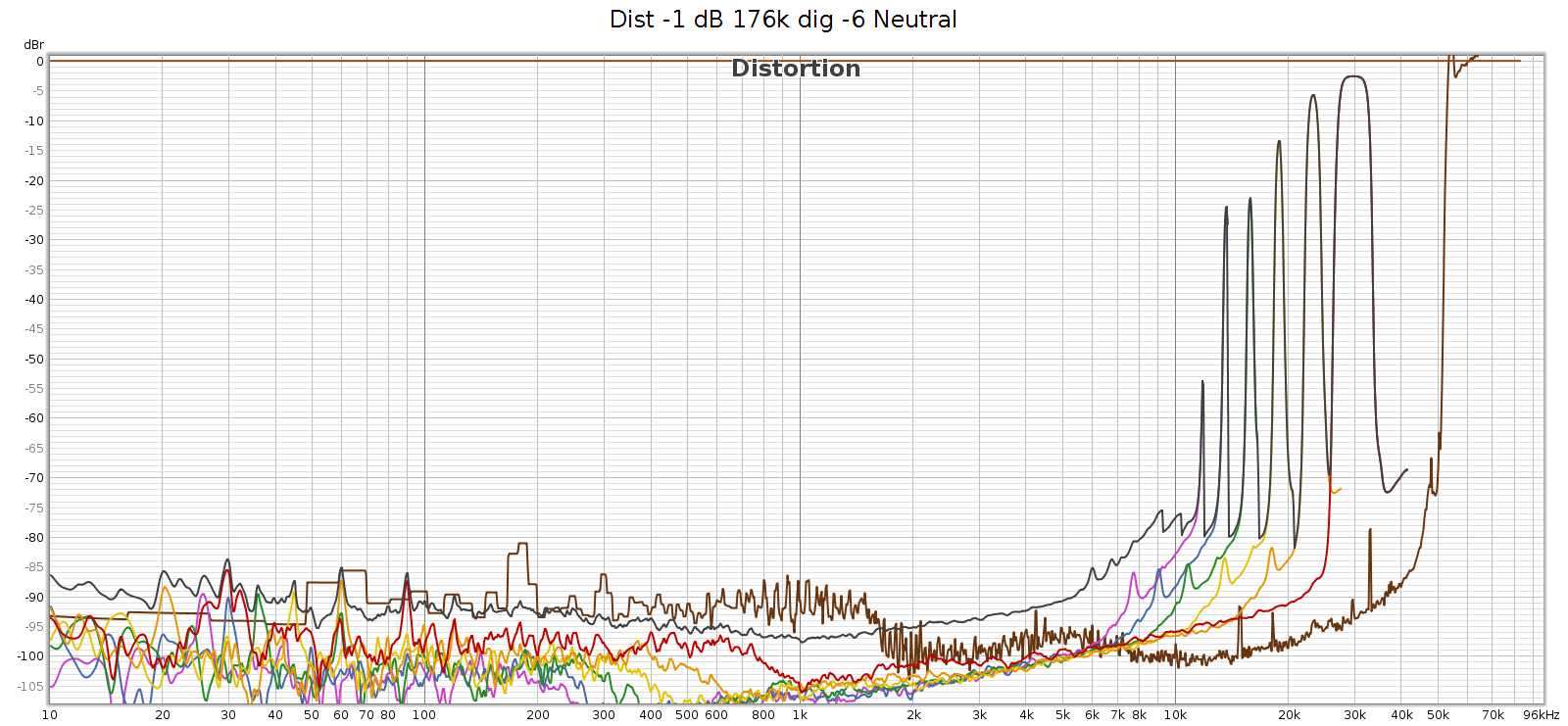
At 176.4k, it’s clean up to 11 kHz and that first distortion spike is at 11,960 Hz. This is inaudible since it’s 7th harmonic so the distortion tone is at 11,960 * 7 = 83,720 Hz. However, these distortion spikes are big enough that their intermodulation (IM) differences are in the midrange. They are spaced 1-3 kHz apart, which puts the IM smack-dab where our hearing is most sensitive to it.

Here’s what it looks like at 192 kHz:

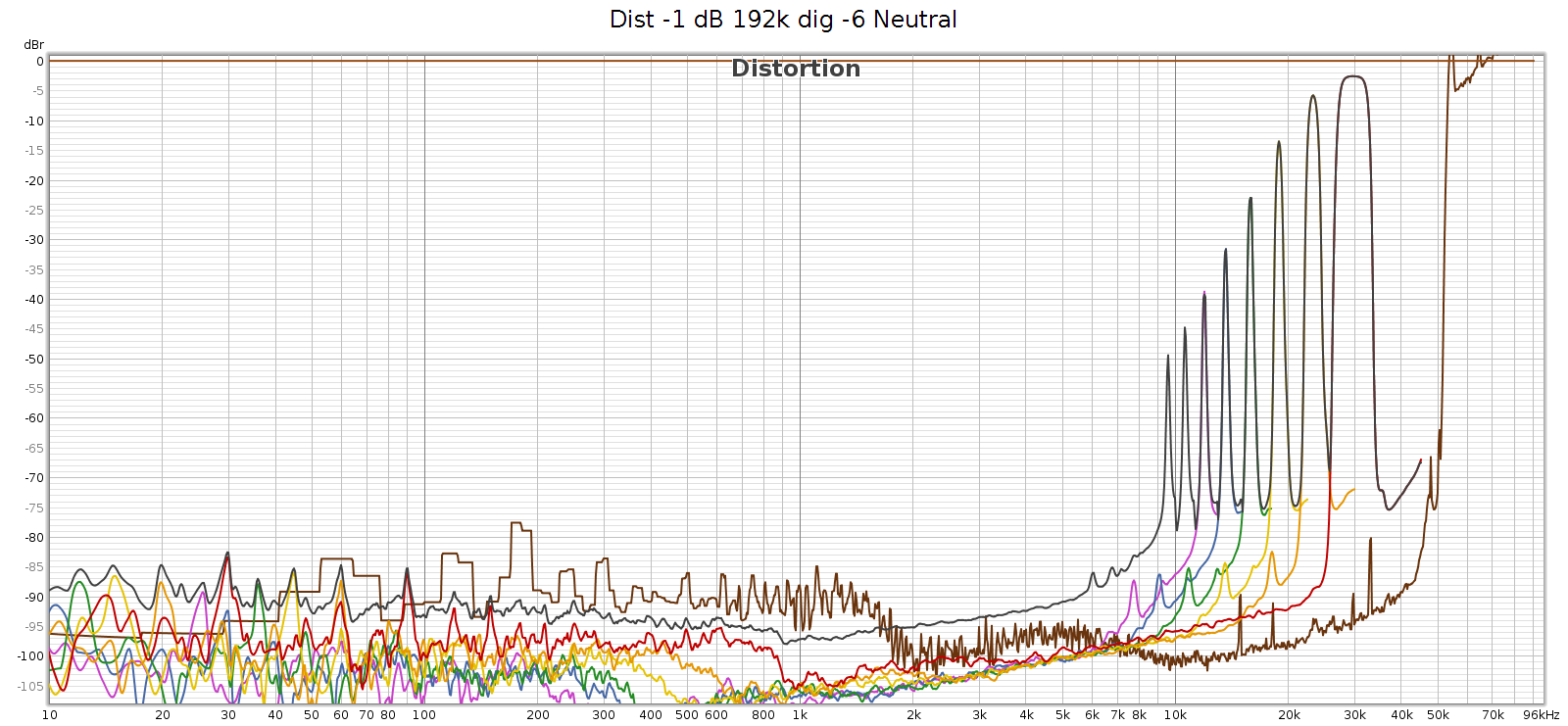
At 192k we have a similar situation, first distortion spike at 9,580 Hz, which will be inaudible since it’s 9th harmonic so the distortion tone is at 9,580 * 9 = 86,220 Hz. The 7th, 6th, and rest of harmonics are the same as at 176.4k sampling. And as above, the IM difference tones will be in the midrange.

Two interesting observations about these frequencies:

  1. They are exactly the same at 176.4 and 192 kHz. This suggests it is noise, not distortion – it’s not correlated with the signal.
  2. They all point to noise in the same region: 53 to 86 kHz

More precisely:

  • H9 @ 9,580 Hz means a frequency at 86,220 Hz
  • H8 @ 10,620 means 84,960
  • H7 @ 11,960 means 83,720
  • H6 @ 13,640 means 81,840
  • H5 @ 15,870 means 79,350
  • H4 @ 18,940 means 75,760
  • H3 @ 23,320 means 69,960
  • H2 @ 30,000 means 60,000

Here’s my speculation as to the root cause. Something in the COUNTry (perhaps a switching power supply?) is operating at 65 kHz. This is not fully suppressed or filtered and is leaking (somehow?) into the digital data. At sample rates 96k and lower, it’s above Nyquist and thus digitally filtered. But at 176.4 and 192, it’s below the Nyquist limit of 88.2 and 96 kHz respectively, so it is in the passband. Thus this power supply switching noise appears as harmonics of the given lower frequencies. If so, then it’s not really distortion, it’s noise.

Wherever the source of this noise, it’s interesting to study it closer. I created another graph below for this. Noise goes through the roof (literally – greater than 100% or louder than the fundamental) with spikes at 54.6 and 65 kHz. This noise profile and the spike frequencies are exactly the same at 176.4 and 192 kHz, so it’s independent of sampling frequency. It looks like this noise is what the graph (incorrectly) shows as distortion. Each of the N harmonic spikes is simply that same noise frequency divided by the next larger number (2nd, 3rd, 4th, etc.). Note that noise above the 0 dB line is not a bug. The spike at 65 kHz at +10 dB means it’s 10 dB louder than the signal.

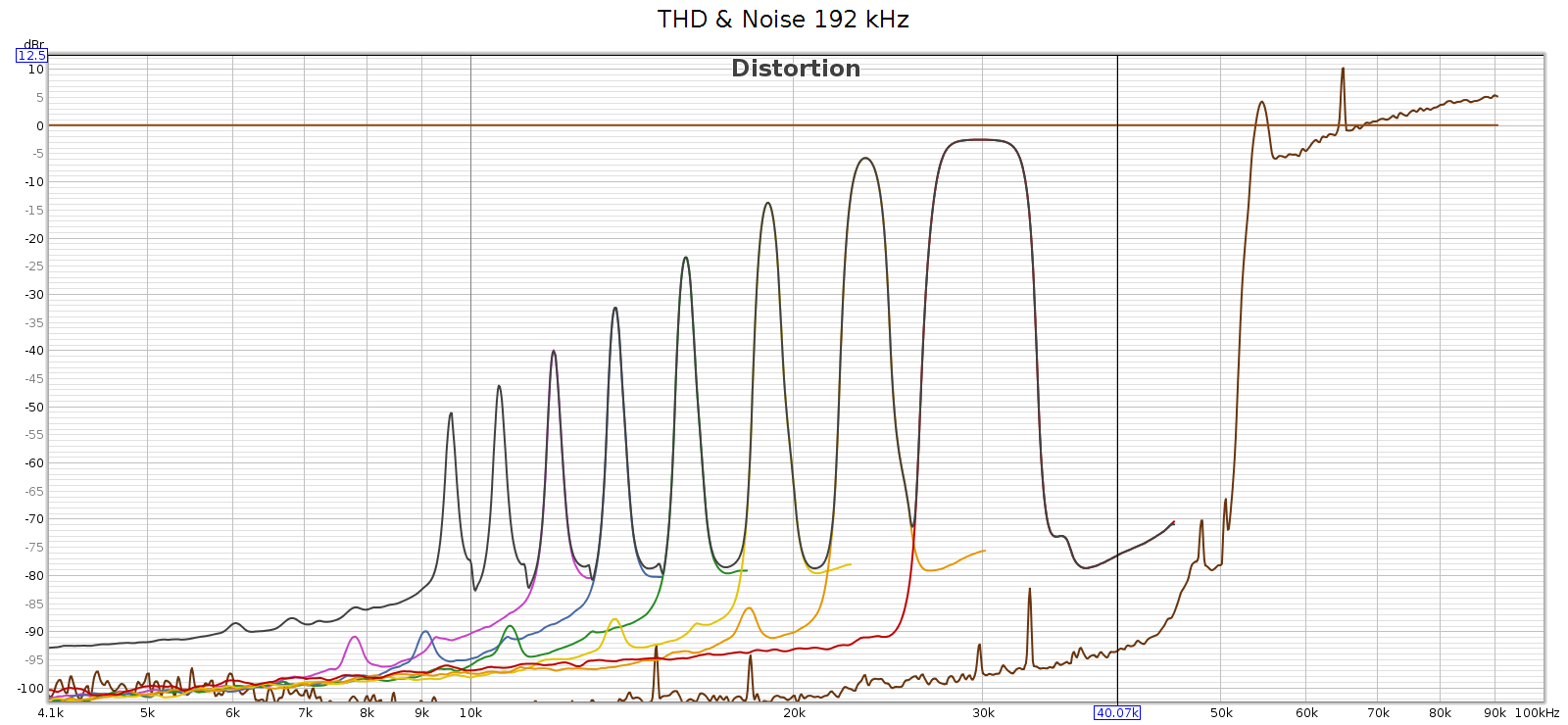
In case this noise were caused by the high level of the digital signal (even though it wasn’t clipping), I ran another sweep at -48 dB. The noise profile looks the same:

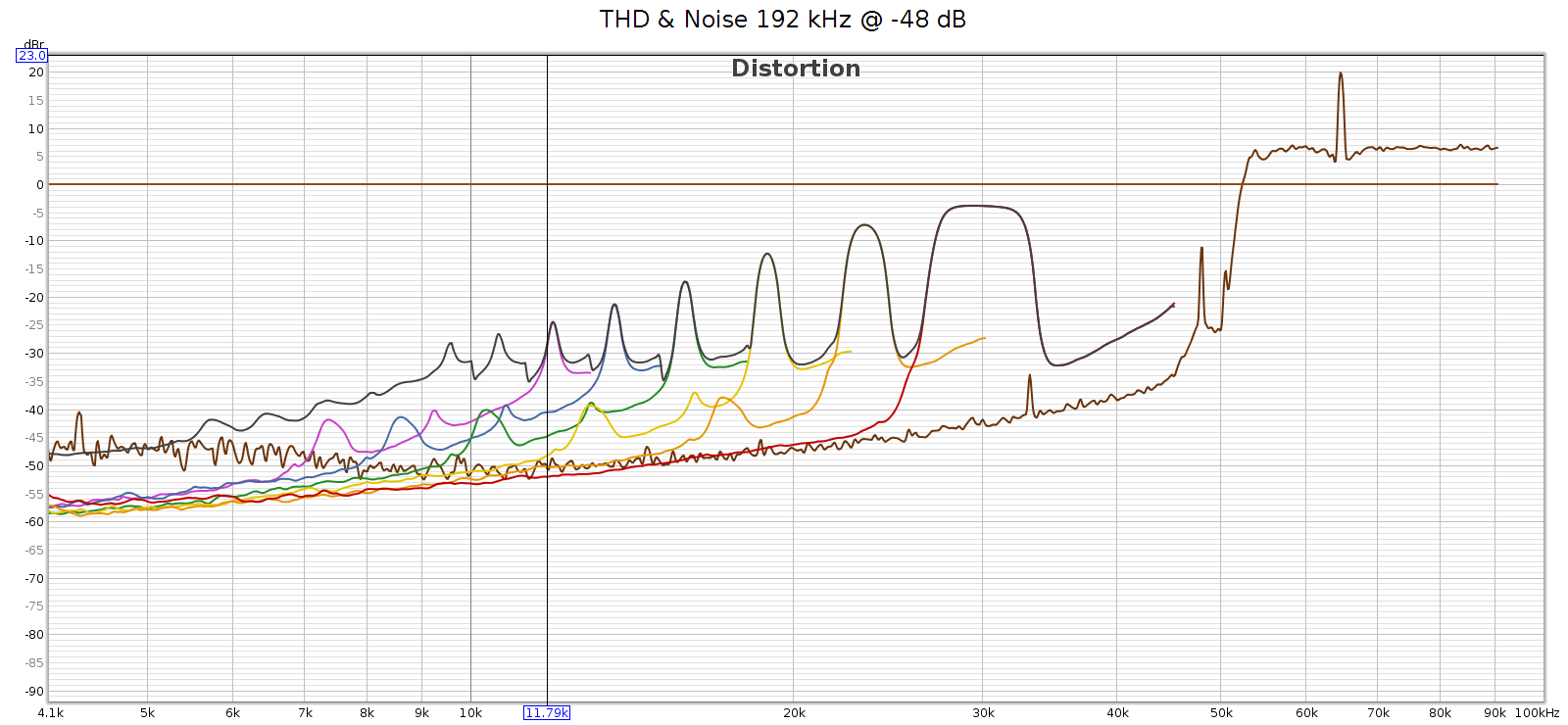
In short, the noise is a constant level, and a constant frequency spectrum. It’s independent of the sample rate and of the input signal. This suggests it’s noise not distortion.

I said earlier that I was speculating – let me clarify. What is not speculation, but observation, is a lot of supersonic noise at high sample rates. My speculation is toward the root cause. I love a good puzzle and this explanation fits the observations. But I don’t really know what is causing that noise. So let’s set root cause speculation aside…

For comparison, here’s the COUNTry distortion and noise at 96 kHz, measured at the analog outputs at medium gain: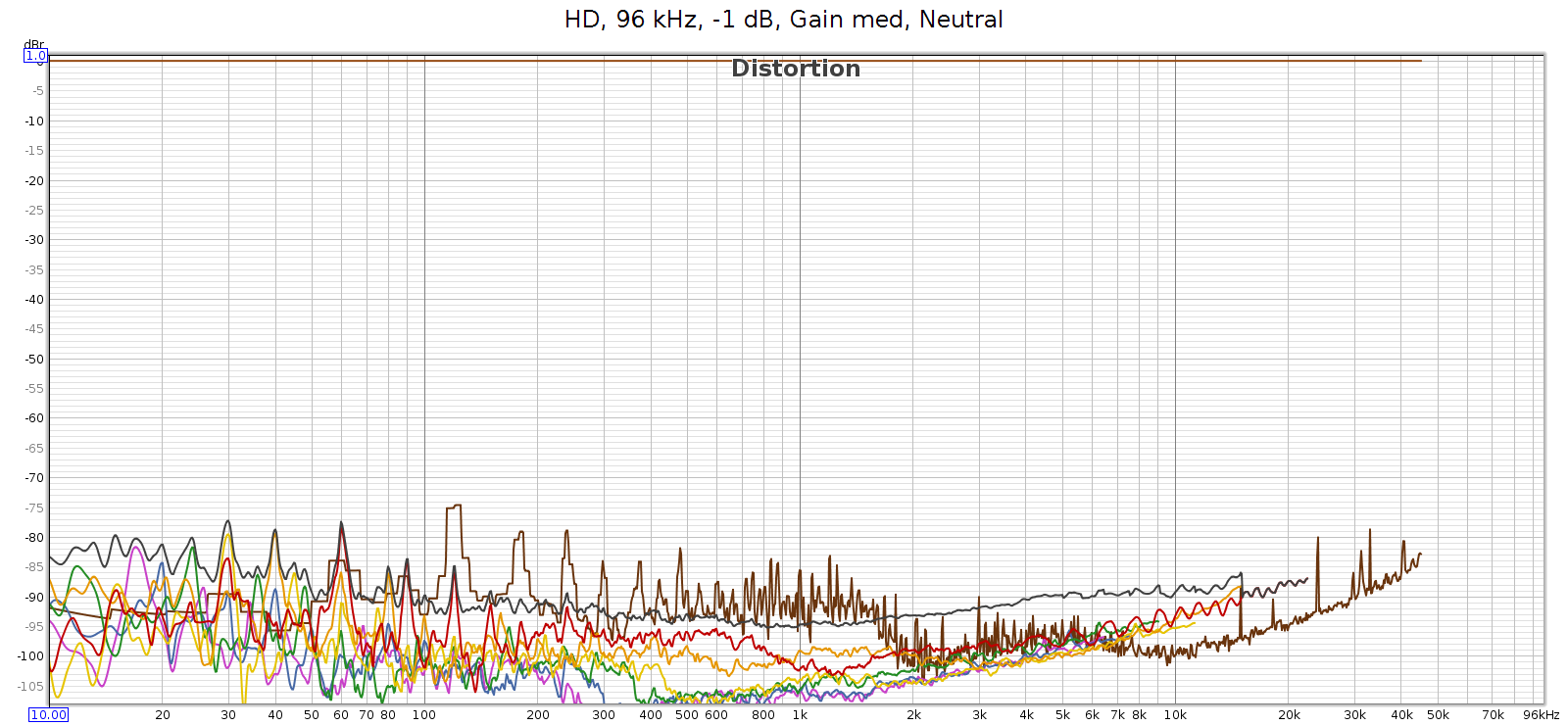

BTW, see that drop in noise & distortion from 700 to 2,000 Hz? I’m guessing this is the previously mentioned FF at work.

Here’s the distortion and noise of the measuring system, my ESI Juli@ sound card in loopback:

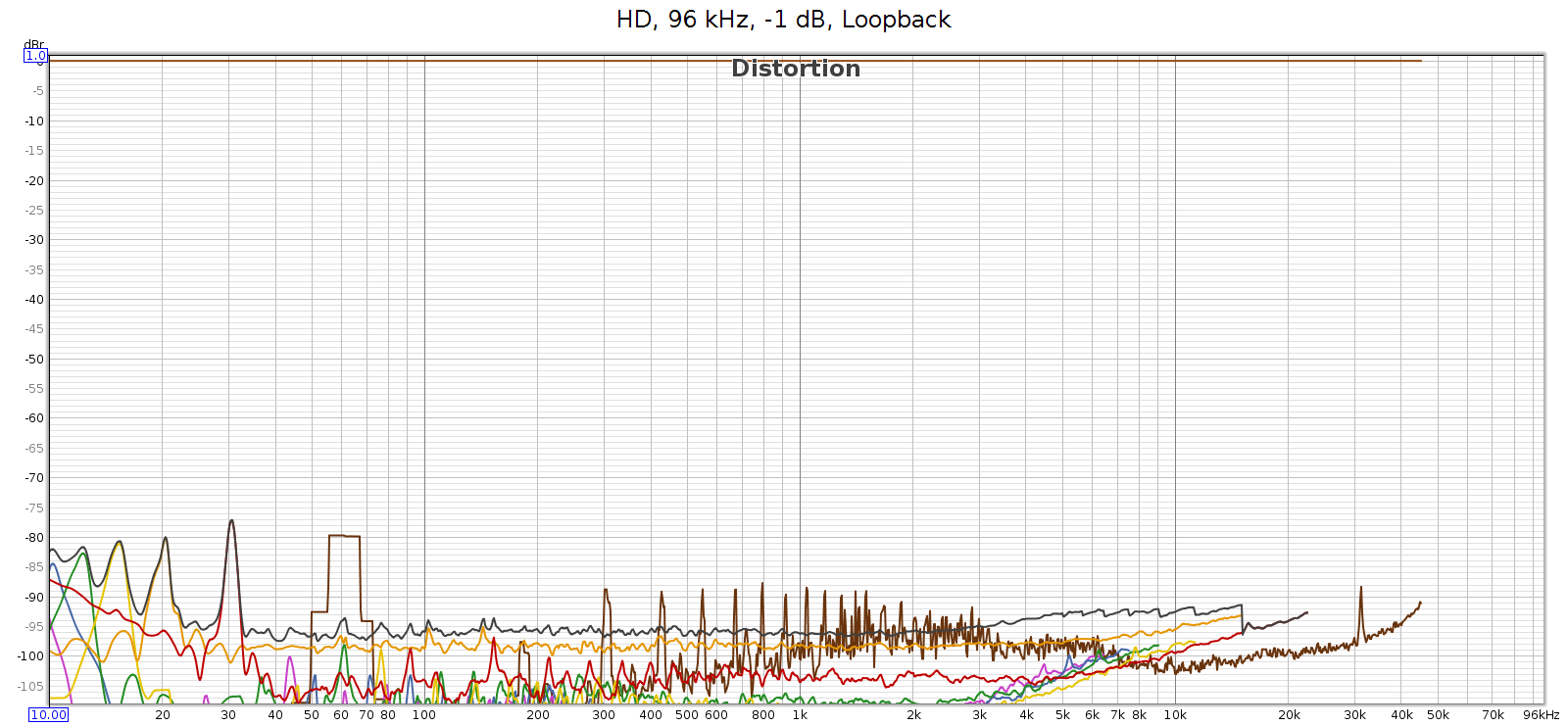
This typical of all sample rates 96 kHz and lower. So the COUNTry’s D/A and analog output is pretty clean – just a bit higher than the loopback connector, but not much. This should be well below audible levels.

Finally, I used Audacity to under-sample the 192 kHz test signal to 96 kHz, then played it through the COUNTry. The output looked clean, just like the 96k signal above. As expected.

Just in case the issue was with the 192 kHz tone itself, I measured how the SMSL SU-6 reproduces that test sweep signal, directly without the COUNTry. You can see those rising harmonics, but they cut off around -80 dB. This is the inherent noise and distortion of the Juli@ card’s analog input and A/D converter.

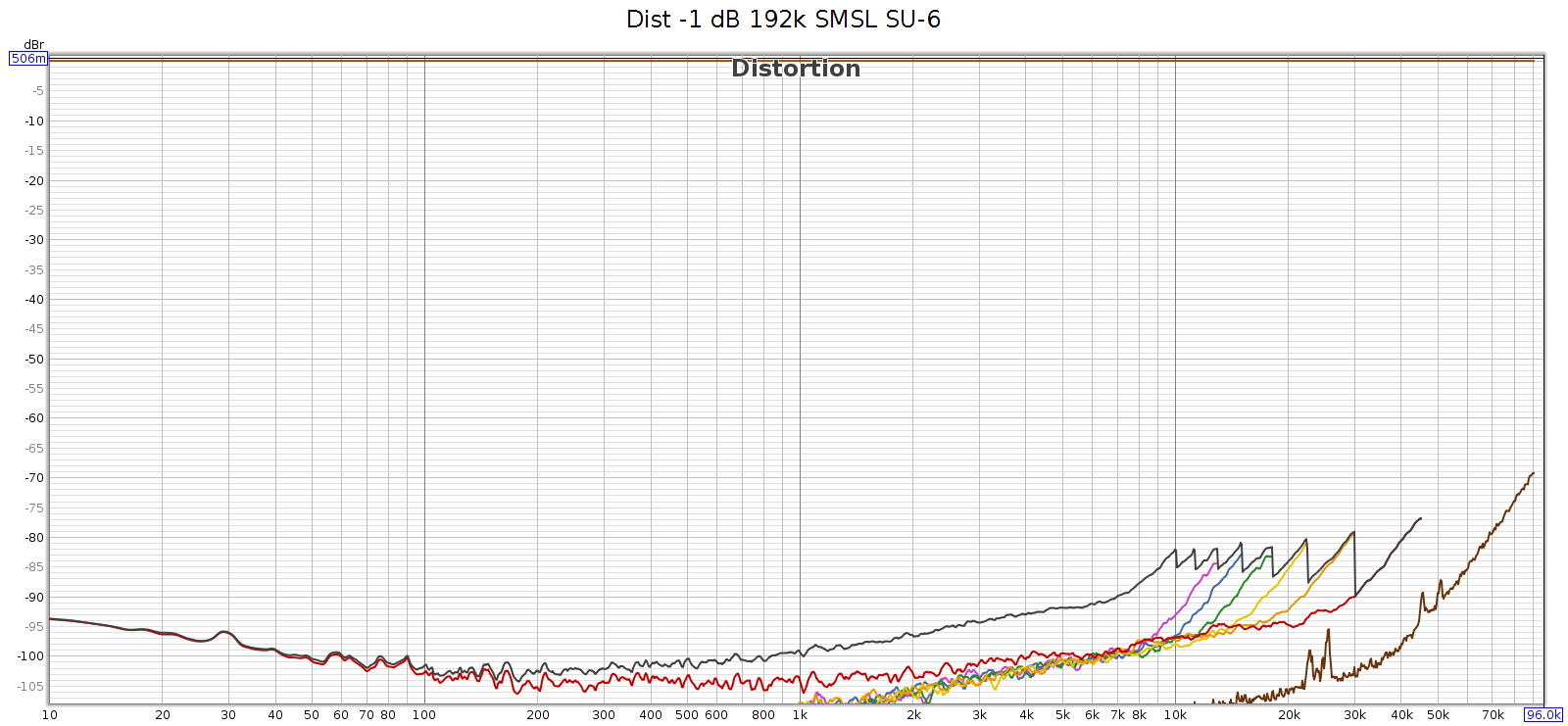
Conclusion

The COUNTry is a unique device. At 1 kilobuck it’s rather pricey, but considering its functionality, as an all-in-one device it replaces several others: DAC, amp and EQ with DSP. If you bought these separately, the total cost might be similar. And the COUNTry’s DSP features are unique and well implemented – you might not be able to find such a flexible EQ, or DSP with crossfeed or reverb. It’s built to last and the sound quality, both measured and subjective, is quite good if not state of the art. Used in purely digital mode, it should be sonically transparent, at least up to 96 kHz.

Meier Audio sent me one on request because I was curious about it. I don’t get to keep it. Yet over an extended trial using it nearly every day, here’s what I like best about it:

  • The flexibility of the EQ (shifting center freqs by combining adjacent bands) enables me to match the LCD-2F and HD-580 headphones, and most others.
  • The crossfeed is nice especially with albums having hard-panned L-R stereo separation.
  • Flexibility to be an all-in-one device or run in digital-only mode.
  • Works with my various audio systems with no observed software/firmware bugs.
  • Good quality, seems built to last with good support.

Suggestions for improving the COUNTry:

  • Fix the HF noise/distortion issue at high sampling rates.
  • For improved transparency, make a version that run DSP at the native sampling rate of the source without resampling.
  • If native rate processing is not possible, then over or under sample at integer multiples. Example:
    • Implement all internal functionality at 2 rates: 88.2 & 96
    • Input at 44.1, 88.2 and 176.4 process at 88.2
    • Input at 48, 96 and 192 process at 96
  • Provide an indicator when CD de-emphasis is activated (perhaps change the color of the 16k EQ band).
  • Eliminate the bass attenuation in high gain mode.
    • Sure you can normalize it with bass boost, but better to give it flat response like low & medium gain.
    • Not really an issue for me, since low gain is plenty for my headphones.
  • One of the nice things about the COUNTry is that due to the physical knobs you can see all the modes at a glance. But the knob detents are hard to see. If I owned this device I’d fill the detent notches with white paint.

Of the above, the the only thing holding me back from buying one for myself is the first 2 items. Eliminating the high frequency noise and not resampling might also improve the clarity / transparency / sound quality.

Meier Audio makes another version of the COUNTry that resamples everything to 96 kHz instead of 192 kHz. This 96k version has a more complex implementation of bass boost, called bass enhancement. It’s quite an interesting feature that leverages the psychoacoustic phenomena known as the “false fundamental”. As cool as that is, this 192k version has certain advantages, even if one doesn’t care about the difference in sample rate:

  • Bass boost exactly offsets the analog bass attenuation at high gain. The 96k version has no way to do this, since it replaces boost with enhancement.
  • Bass boost closely offsets the bass attenuation of several headphones, especially the Sennheiser HD 580/600/650/800 models.

Note that neither of the above reasons has anything to do with 96k versus 192k sample rates. In my opinion, 192k offers no real advantage over 96k because whatever advantages are gained from rates higher than the 44.1k CD standard, are fully realized at 96k.

Update: Apr 2023

Meier audio has a new version of the COUNTry:

  • Performs all DSP at the native sample rate (32, 44.1, 48, 64, 88.2, 96, 128, 176.4, 192)
    • Digital-only mode has no resampling, should be fully transparent
  • D/A conversion is always done at 96k, since the WM8716 chip is optimized for this rate
    • The analog audio output is resampled to 96k before D/A conversion
  • Equalizer step sizes are 0.5 dB resolution
  • Reverb replaced with 3 levels of bass boost (50 Hz shelf, Q=1.0) +2, +4 and +6
  • The original bass boost (45 Hz shelf, Q=0.5, +6 dB) is retained, and can be applied in addition.

Analog vs. Digital

Audio, Math, Tech
by Mike Clements

From Merriam Webster:

Analog

  1. of, relating to, or being a mechanism or device in which information is represented by continuously variable physical quantities
  2. something that is similar or comparable to something else either in general or in some specific detail : something that is analogous to something else

Digital

  1. composed of data in the form of especially binary digits
  2. of, relating to, or using calculation by numerical methods or by discrete units

In terms of storing, transmitting and playing audio, each term is ambiguous, yet their different meanings are similar, which leads to confusion.

Analog

The key phrase with meaning 1 is “continuously variable”. A turntable needle tracking a record groove, a tape deck head responding to fluctuating magnetic fields on tape, are both continuously variable. Reflective and non-reflective spots on a CD are not continuously variable – it either reflects a laser beamed at it, or it doesn’t. A square wave transmitted along a wire is not continuously variable – it is either at its max voltage, or its min voltage, nothing in between.

However, if we look more closely at the last two examples, we realize that they really are continuous. A reflective spot on a CD doesn’t reflect back 100% of the light; it’s not perfectly smooth, some of the light is scattered and lost. Conversely, a non-reflective spot does reflect back some tiny amount of the light, even though it absorbs or scatters most of it. And while all the spots of the same type (reflective or not) are similar, they are not exactly the same; each is unique. A square wave does not switch from high to low, or low to high, instantaneously. That would require infinite rise time, which is impossible. And as it approaches the new voltage, it will overshoot or undershoot just a bit before it stabilizes. So the voltage actually does vary continuously from the high to low value, even if it spends 99.99% of its time at a high or low value. In this sense neither of these are as discrete as they first seem; they are almost but not quite discrete, but actually continuous.

In fact, the universe at the super-macro atomic scale at which we perceive and manipulate it, is continuous. It only becomes discrete at the subatomic/quantum level.

The other sense of “analog” is that it is an “analog” of, or actually resembles the thing it represents (closely related to the word “analogy”). A magnetic tape that encodes music, has a strong field where the music is loud and a weaker field where it is quiet. A turntable needle tracking a record groove physically moves over a bigger amplitude when the music is loud, smaller when it is quiet. The shape of the groove itself resembles the waveform of the music being played.

Music as we experience it, and as it passes through air as vibrations and pressure changes, is continuously varying. Analog storage of music fulfills both definitions of the term: it is continuously varying, and it physically resembles the music (in some way, directly or indirectly).

Digital

The first definition refers to binary digits. However, this does not fully capture the sense of what it really means. The rational numbers are continuously varying, in the sense that they are infinitely dense: between any two of them, no matter how close they are, lie infinitely many more. Mathematically, the rational numbers are not a true “continuum”, as they have holes – by holes I mean numbers that we know must exist since they are the solution to simple algebra problems, yet are not rational. For example, the square root of 2.

Yet pragmatically speaking, this is a distinction without a difference. It is impossible to detect the difference between rational and real numbers through observation or measurement of the physical world. For every irrational number R, for any small value ε, we can pick a rational number Q so that | R – Q | < ε. We can pick ε smaller than any means of physical observation or measurement. Indeed, ε can be smaller than relativistic uncertainty principles permit. So even in theory, not just in practice, it is impossible to discern the difference in the physical universe. The difference between rational and real numbers does exist, but it is a mathematical distinction, not a physical one.

So for purposes of analog vs. digital, the notion of “infinitely dense” is a sufficient interpretation of what “continuous” means. Numbers can be continuous. Of course, numbers can also be non-continuous or discrete: like the counting numbers.

Even binary digits can be continuous. Every rational number can be expressed in binary digits, though some of them require infinitely many binary digits. For example, 1/7 in binary is 0.001001001… but that is still a well defined and valid number. When people use the term “binary digit” they often mean stored in a computer. But binary is simply a numbering system. It can be, but doesn’t have to be, stored in a computer.

However, in a computer the manifestation (storage, transmission, computation) of numbers is necessarily finite. Thus these numbers cannot be “infinitely dense”, which means they cannot be continuous. They are discrete numbers – even floating points, because they have finite resolution.

Because numbers can be either continuous or discrete, they are a poor concept on which to base the definition of “digital”. So much for Webster’s definition 1; that colloquial usage leads to confusion.

A better concept is definition 2: that of being “discrete units”. Storing or encoding data as a set of discrete states. We often use computers and binary, but the number of states is immaterial: it can be 2 (binary), 3 (trinary) or whatever.

In short, a big part of the confusion around the term “digital” is this: Just because it uses numbers, doesn’t mean it must be discrete. And just because it’s discrete, doesn’t mean it must use numbers.

Digital audio is discrete, and it uses numbers. The first is essential, the second is an incidental convenience.

Once again: truly discrete phenomena do not exist in our universe at the super-macro atomic scale. Discrete means a set of states with nothing in between the states. This is easy to understand from an abstract logical perspective. But shifting between physical states cannot be instantaneous, because that would require an infinite rate of change, which requires infinite energy/power.

Manifestation vs Meaning

Put differently: what it is vs what it means

Put differently: the signal, versus the information

A signal is a phenomena in the physical universe that encodes information. The signal can be a radio wave, a telephone transmission, handwriting on paper, scratches on a clay tablet, etc. Signals contain or encode information. The sender translates or encodes the information into the signal. The receiver decodes the information from the signal.

All signals are continuous, by the simple fact that they exist in our universe which does not have discrete phenomena at the macro-atomic scale. But this does not imply that all signals are “analogues” of the information they encode. Some are, some are not. That depends on the encoding.

The same signal could have different meaning, depending on the encoding. If the sender and receiver do not agree on the encoding, they may believe the message has been successfully transmitted, when it has not. The receiver might decode the signal in a different way than the sender encoded, and thus receive a different message.

This illustrates the fact that the signal, and the message or information it contains, are two different things. One is physical, the other logical. Signals cannot be discrete, but messages/information can be either discrete or continuous.

We can encode discrete messages into continuous signals. For example: consider the discrete binary message 11111100110 (which happens to be 2022, the current year). We can encode this into a series of voltage pulses each of fixed duration, encoding each 1 as 1.0 V and each 0 as -1.0 V. The receiver can easily extract the 1s and 0s from the signal.

However, somebody who doesn’t know the encoding scheme may receive this signal and not even know whether it contains a message, let alone what that message is.

Advantage: Digital

So what is the big deal behind digital audio? Why back in the 1980s was it called “perfect sound forever”? It’s neither perfect nor forever, so where did that phrase come from?

When encoding information into a signal, and decoding it from a signal, discrete states have certain advantages over continuous varying. Consider the above example of positive and negative voltage pulses. The receiver doesn’t care exactly what the voltage is. He can interpret any positive voltage as a 1, and any negative voltage as a 0. If the signal gets distorted, like a bunch of ripple added to it, or the peaks vary between 0.7 and 1.3 instead of exactly 1.0, it won’t change the message. The receiver will still receive it perfectly intact. Of course, under extreme conditions the signal could be so distorted that the message is lost, but that takes a lot of distortion. Encoding information as discrete states is robust, and in most normal cases delivers perfectly error-free messages.

Now consider an analog encoding of information, like a turntable needle tracking a record groove or a tape deck head detecting the magnetic field on tape passing by. Here, the encoding is continuously variable. Every tiniest wiggle or variation has meaning, it is part of the message. Indeed, high quality audiophile equipment is designed to respond to even those smallest subtle signal changes. If the signal gets distorted, even slightly, the distortion becomes part of the message. This encoding is not robust; it’s much more difficult to tell the difference between the encoded message, and any distortion that signal may have suffered.

Summary

For precision, let’s use “discrete” instead of “digital” and “continuous” instead of “analog”.

Digital audio is information. The original music is a continuous phenomena, and is encoded into information as discrete states. Those discrete states are encoded into continuous form for physical storage and transmission, and can be decoded back into discrete states. We use this discrete encoding because it is more robust, relatively immune from imperfections and distortions in transmission and storage, which makes possible perfect transmission that is not possible with information encoded in continuous forms.

In short, digital audio is “digital”, but the means by which we store and transmit it is “analog”. We encode the digital audio information into analog form or signals, and decode or extract the digital information from the analog signals.

The theory and physics of discrete vs. continuous information and signals has been known since Claude Shannon and others developed information theory back in the early 20th century. The Shannon-Whittaker interpolation formula which is the basis for analog to digital to analog conversion, was known at least since the 1930s. So why didn’t digital audio exist until the 1980s? The reason is computing power – or lack thereof. The range and resolution of human hearing is high enough that it requires a lot of digital data to attain sonic transparency. We knew how to do it, but it took decades for computing technology to get fast enough to process the volume of digital data required.

Goodbye Arvixe, Hello Hostgator!

Tech
by Mike Clements

TLDR; this site is now hosted on Hostgator. Previously was hosted on Arvixe

I registered the mclements.net domain name back in 2001 or so, over 20 years ago! At first it was on register.com. Then switched to GoDaddy for several years. Then switched to Arvixe for several years. Recently (June 2022) switched to Hostgator.

The first 2 switches were due to price. As I gained experience with hosting (web, ftp, email) I didn’t need the services or support; all I wanted was the servers to be up and reliable. Yet the last most recent switch was due to service & support.

The Rest of the Story…

Starting in late April 2022 I was intermittently unable to access my site or email. No error messages, no response from the servers, network timeout. They appeared to be down. I opened tickets with Arvixe and they always said the servers were up, try again. I would try again, they were not up, so I reopened the tickets. This game of trouble ticket ping pong went on for a few frustrating weeks. Around this time I was returning to the office and realized that my site and email always worked from the office.

Now I had a clue what might be happening: blacklisting – or now that we are changing our terminology to be more inclusive, blocking. I assumed it must be Comcast (our ISP) blocking Arvixe servers. Why? This had happened before over the years, other service provider blocking our emails. I notified Arvixe and they contacted the providers to get off their block-lists.

But this time was different. First, all I could get from Arvixe support was the same canned response over and over: “it works from our end, try again”. They would not acknowledge my suggestions that my sites were being blocked. It was as if they had no support, just robotic answers to tickets. Second, I contacted Comcast and submitted a request to un-block my web site (this link). But this seemed unlikely – if Comcast doesn’t block sites with porn or other offensive material, why would they be blocking my family web site?

Finally I gave up. Arvixe was never going to fix the problem. I researched different hosting providers and picked Hostgator. I used Arvixe CPanel to back up my entire site (including FTP and email) to a giant TGZ file and downloaded it (over 30 GB!). After opening my Hostgator account I gave them access to my Arvixe site and they migrated everything. Site, WordPress, FTP, email, you name it – everything. It was over 60 GB of data.

Transferring the domain registration was a pain. There was no way to do this in the Arvixe UI, so I had to contact support. They sent me the security code to do the transfer. Then the transfer would take almost a week.

After the transfer everything worked great. Until the next day, I had the exact same problem – I could not access the site from home, but I could from work. My site was blocked again!

I used these sites to see if the site was down for everyone, or just for me:

https://downforeveryoneorjustme.com
https://isitdownorjustme.net

Of course the site was up, just not for me. So my IP was being blocked. It must be Hostgator. I contacted their support. Within 15 minutes the agent checked my account and said yes, we’re blocking your home IP addr due to failed logins. And he whitelisted my home IP addr. So much better support than Arvixe ever had. But how could there be failed logins from my home IP addr? AHA! I thought – I must have old email clients running on some random device that is constantly retrying to login and failing. I went through all my devices at home: phones, tablets, computers, etc. to ensure all of them had the correct credentials for my site. Then the site was up for a couple of days straight, no problem.

Then I went to reconfigure my FTP client, got the password wrong once – and my site was blocked again. I contacted Hostgator support. This agent was nowhere near as knowledgeable as the first. I spent over 30 frustrating minutes trying to convince him that Hostgator was blocking my IP addr. The agent said Hostgator wasn’t blocking me, it must be my browser or my ISP. Finally, to prove he was right, the agent ran an internal Hostgator tool to check my home IP addr and showed me the output. Of course, within that 100+ lines of output was a line showing my IP addr saying “BLOCKED”. So the agent finally realized I was right all along. My IP addr was on the “temporary” blocklist so all I had to do was wait for an hour or two and then it would work – and it did!

Conclusion

In summary, here’s what seems to have happened:

  • In late April, the cPanel based hosting software made a security change, adopting a more aggressive blocking rule. The new rule: a single failed login causes a 1-2 hour IP addr block. During this time, if more failed logins are attempted, it becomes a permanent block.
  • Hosting companies (Arvixe, Hostgator, etc.) don’t know about this change. They still tell customers that it takes something like 10 failed attempts in 10 minutes to trigger it. That is incorrect.
  • The cPanel based hosting software does not allow account owners to configure this. It is only available to hosting company engineers.
  • Arvixe still doesn’t know about this change.
  • Hostgator does – I’ve told them about it and they’ve said they will train their agents.