Introduction
This is about passive attenuators. Sometimes called “passive preamps”, they are switchboxes with volume controls that typically have 24 to 128 discrete positions. Back in ’00 I designed and built one, and used it daily for over 10 years.
Passive attenuators get a mixed reaction from audiophiles. Some say they are the most transparent way to listen to music, better than any active preamp at any price. Others say they sound un-dynamic and flat. Audiophiles with EE backgrounds also have a mixed reaction to them. Some say they are transparent, others say they have high noise and non-flat frequency response.
In this article I’ll describe
- System requirements for a passive to work well
- How a passive actually works
- Measurements of noise and frequency response comparing their performance to the best active preamps
- Comparison to active preamps
1. System Requirements
It turns out all the above views have some thread of truth. How well a passive works depends on the system in which it is used. Here are the requirements:
- Upstream devices (sources) have low output impedances
- Downstream devices (destinations) have high input impedances
- Short cables having low capacitance
- Sources are “loud” with enough gain to drive destinations to full power
Put differently
- You don’t need gain, you only need attenuation.
- All your devices, upstream & downstream are solid state.
- If you plug your sources directly into your power amp, it will drive it to extra loud levels you will never actually use.
Most solid state components and well engineered cables meet these requirements. A system that doesn’t meet these requirements is the exception, not the norm.
2. How a Passive Attenuator Works
A passive attenuator is a simple voltage divider. The source device signal is a voltage swinging from + to -. Send this voltage through 2 resistors in series, R1 and R2. The downstream device receiving the signal is in parallel with R2.
The voltage will have some drop across R1, and some drop across R2. How much it drops across each resistor depends on their impedance ratios. This determines the volume setting: how much it attenuates the signal.
The passive attenuator’s volume knob has a fixed number of discrete positions, typically spaced 0.5 to 2 dB apart. For example 24 positions about 2 dB apart, or 64 positions about 0.5 dB apart. Each position puts 2 different resistors in the signal path.
Before going further, let’s mention 2 simplifying assumptions:
- The source device output impedance is zero
- The destination device input impedance is infinite
These are not actually correct, but they are close enough. Most solid state sources have output impedances around 10 to 100 ohms. Most solid state amps have input impedances around 10,000 to 50,000 ohms.
2a. Source Load
The passive attenuator shows the same load (impedance) to the source device at every volume position. So the source doesn’t “care” what volume position you are using. Make this load high enough that it is easy for the source to drive it, but no higher. The source has to swing a voltage back and forth, and the higher the load impedance, the less current it draws. So higher impedance is an easier load. But too high an impedance creates higher noise (more on that later).
A 10k attenuator means R1 + R2 = 10,000 ohms at every volume position. A 5k attenuator mean they sum to 5,000 ohms. The most popular attenuator is 10k, though 5k and 20k are also used. From here on we’ll talk about 10k, but the reasoning can be applied to any value.
As a general rule, you want at least a 1:10 ratio from the source to the load. If the source has a 100 ohm output impedance, it wants to drive a load of at least 1,000 ohms. Typical solid state sources are less than this, so a 10k attenuator gives more than 1:100 ratio which is more than sufficient. If all your sources are under 500 ohms output impedance, then you should use a 5k attenuator.
Since R1 and R2 are in series, the total load the source sees is R1 + R2. Of course it’s a little less than this since the destination device is in parallel with R2 which lowers the resistance across R2. But its input impedance is so high it doesn’t materially affect it.
So now we have the first rule of a passive attenuator: each pair of resistors R1, R2, sum to 10,000 (or 5k, or 20k).
2b. Attenuation
We mentioned earlier that the ratio of R1 to R2 determines the attenuation. Here I’ll explain exactly what that means.
At every volume position, the total load is 10,000 ohms. If R1 makes up half of that, then half the voltage drops over R1 and the other half drops over R2. In this case, if the source signal is 2 V, then 1 V drops over R1 and 1 V drops over R2. If R1 makes up 75% of that, then 75% of the voltage drops over R1 and 25% drops over R2. In this case if the source signal is 2 V, then 1.5 V drops over R1 and 0.5 V drops over R2.
We convert these ratios into dB with the standard formula
20 * log(ratio) = dB
More on that here.
It just so happens that the first example above is -6 dB of attenuation, and the second is -12 dB. That is:
20 * log(0.5) = -6 20 * log(0.25) = -12
Converting this intuition into math, this leads to the formula:
Attenuation Ratio = R2 / (R1 + R2)
Since R1 + R2 is always 10,000 this gets even simpler. If you want to attenuate the signal to, say, 17% of its original value, use a 1700 ohm resistor for R2, then R1 will be the difference between that and 10,000.
This is all there is to designing a passive attenuator — at least, to selecting the resistors for each volume position. Their ratio determines the attenuation, and their sum is always 10,000. You can get fancy and include the actual impedances for the source output and destination input, but it won’t change things much.
2c. Wrap Up
What input voltage does the downstream device see? It’s the output voltage of the attenuator. The circuit diagram makes it obvious:
The downstream device is in parallel with R2, so it sees the same voltage. The voltage drop across R2 is the output voltage, which will always be equal or less than the source voltage (since some of the voltage will drop over R1).
The diagram shows resistors for -32 dB of attenuation, or the output being 2.5% of the input.
Example: let’s compute the first few highest volume settings for a passive attenuator having 24 positions each 2 dB apart.
Position 1: full volume. Here, R1 is zero – just a straight wire and R2 is 10,000 ohms. The entire signal (2 V or whatever) drops across R2.
Position 2: -2 dB. First, compute the ratio for -2 dB. Reversing the above formula we get:
10^(-2/20) = 0.7943
This means R2 is 7,943 and R1 must be 2,057.
Position 3: -4 dB. Our ratio is 0.631, so R2 is 6,310 and R1 is 3,960.
Now resistors aren’t available in arbitrary values. You would look at the parts list and find resistors that come closest to the values you want. In practice, when designing an attenuator you can usually get the steps within 0.1 dB and keep the total resistance within 100 ohms (or 1% of your target value).
Congratulations – you can now design a passive attenuator!
The next question is: why would you use one? One part of that answer is low noise at low volume settings.
3.1 Noise
Resistors add noise to the signal. How much noise depends on the type of resistor; some are noisier than others. There is a theoretical minimum amount of noise that any resistor can have; all resistors have at least this much, in fact more. This noise has 3 common names: thermal, Johnson, and Nyquist. But whatever you call it, it is the same thing: the heat energy from the resistor’s temperature, randomly exciting electrons that appear as tiny voltages. We’re talking super tiny here. For our application, it is in micro-Volts (millionths of volts). This noise spans all frequencies, so the amount of noise that is relevant to our application depends on the bandwidth. In audio, let’s assume bandwidth is 20,000 Hz.
A passive attenuator introduces other kinds of noise too. Resistor composition noise, junction/contact noise, etc. To minimize these noises, use high quality contacts and “clean” resistors. The cleanest resistors are wire wound and metal film. These resistors have actual real-world noise so close to the theoretical minimums, we can use those minimums in our noise computations. This isn’t true of other resistor types, which are noisier.
For example, thermal noise of a 10,000 ohm resistor at room temperature in audio bandwidth is about 1.8 uV, or 1.8e-6 volts. A 100 ohm resistor is 0.18 uV, or 1.8e-7 volts. Dropping the resistance by a factor of 100 drops the noise by a factor of 10. If the signal (voltage drop) over the resistor is 1 V, this is -115 and -135 dB SNR respectively. The first is comparable to the noise in the very best active preamps, the second is better than any active preamp. However, if we reach a quiet part of the music and the signal drops 30 dB quieter, the noise level remains constant so the SNR drops by 30 dB and it’s 85 dB and 105 dB respectively.
3.1.1 Noise: Absolute or Relative
When you use a thermal noise calculator you’ll find that resistor noise is measured in 2 ways: as a voltage, and as a voltage ratio. The astute reader will wonder: It can’t be both, so which is it? In other words: Is resistor noise inherently a ratio, so if you apply a smaller voltage across the resistor you get less noise, and the SNR remains constant? Or is resistor noise inherently a constant, so if you apply a smaller voltage across the resistor, the signal is smaller relative to the noise and the SNR drops?
Sadly, for our purposes building passive attenuators, resistor noise is inherently a constant. It is the same regardless of the voltage across or current through the resistor. This suggests that noise is unlikely to be an issue at max volume, but it may become an issue as we turn down the volume.
3.1.2: Noise From What Resistor?
OK so we can compute noise but we’re still not out of the woods. When computing the noise added by a passive attenuator, it’s not obvious which resistor, or more generally what impedance, to use!
For example consider the above circuit diagram. The signal passes through both R1 and R2, so intuition says each one adds noise and the total noise should be the sum of the noise from each. But that sum is always 10,000 ohms, so the noise would always be 1.8e-6 volts. But this simple intuitive approach is incorrect.
3.1.3: Output Impedance
The solution is to view this from the perspective of the destination device. Just like the voltage that matters is the voltage across the destination device’s terminals, the impedance that matters for noise computation is the impedance that the destination device sees. This is called the output impedance of the passive attenuator. Imagine you are at the input terminals of the destination device looking upstream toward the source. What impedance do you see?
Going from + to – upstream, you see R2 in parallel with (R1 and source output impedance in series) . In other worse, the passive attenuator’s output impedance is:
1 / ((1 / R2) + ((1 / R1 + SourceOutput)))
Since output impedance is typically very small, this is close to R2 and R1 in parallel, which is:
1 / ((1 / R1) + (1 / R2))
When R2 and R1 are very different, this is roughly equal to the smaller of them. When R1 and R2 are nearly equal, this is roughly equal to half of either of them.
This is the impedance that determines the noise added by the passive attenuator.
Important note: remember the requirement that the destination device have a high input impedance? You want another 1:10 ratio here. That is, the input impedance of the amp (or your downstream destination device) should be at least 10 times higher than the output impedance of the passive attenuator. The worst-case highest output impedance is when R1 and R2 are equal, 5,000 ohms each at -6 dB. Here the output impedance is 2,500 ohms. So the amp should have an input impedance of at least 25 kOhm.
If it doesn’t, then use a 5k attenuator. But the lower impedance makes it harder to keep the 1:10 ratio on the input side. However, it’s still pretty generous since most solid state sources have output impedances well under 500 ohms.
3.1.4 Computing Noise
Let’s compute the passive attenuator noise from our example above at 0 dB, -2 dB and -4 dB.
At 0 dB, the 2 output impedance legs are 10,000 ohms, and zero. Well not quite zero, but the output impedance of the source device. Let’s suppose that’s 100 ohms. The output impedance will be close to 100 ohms. But more precisely:
1 / ((1 / 10000) + (1 / (0 + 100))) = 99 ohms
Thermal noise of 99 ohms (at room temp and audio bandwidth) we’ve already computed above at 1.8e-7 volts. Also at 0 dB we have the full scale signal from the source, which is 2 V at its loudest which gives us a SNR of:
20 * log(1.8e-7 / 2.0) = -141 dB
Wow! No active preamp achieves that! And it’s probably even better because the output impedance of solid state sources is usually closer to 1 ohm than 100 ohms.
Let’s check the SNR when the music (source voltage level) reaches a quiet part, say 30 dB lower, which is 63.2 mV. Note: we’re not turning down the attenuator, it’s still at 0 dB. We’re just passing a quieter musical signal through it.
20 * log(1.8e-7 / 0.0632) = -111 dB
Well, we really didn’t have to do the math there. Thermal noise is constant and the signal dropped by 30 dB, so the SNR drops by 30 dB. That’s a big drop, but it’s still very good. Again, it’s probably better in the real world because it depends on the the source output impedance will will probably be closer to 1 ohm than 100.
At -2 dB the R1 & R2 resistors are 2,057 and 7,943 ohms. The output impedance will be:
1 / ((1 / 7,943) + (1 / (2,057 + 100))) = 1,696 ohms
Thermal noise of 1,696 ohms is 7.41e-7 V. Per the above, at -2 dB the output is 79.43% of the input. So voltage across R2 (the output voltage) for a 2 V source signal is 1.5886 V. Thus the SNR is:
20 * log(7.41e-7 / 1.5886) = -127 dB
If the music reaches a -30 quiet part, it’s 30 dB worse which is -97 dB.
Now let’s skip -4 dB and use a more realistic listening level. Nobody listens that loud. Typical attenuation for actual listening with a power amp or headphones is around -30 dB. Of course this is a very rough figure depending on amp gain, speaker efficiency, room size and listener preferences. But it’s in the ballpark.
At -30 dB the attenuation is:
10 ^ (-30/20) = 0.03162
So the R2 resistor must be 3.162% of 10,000 which is 316 ohms. That means R1 must be 9,684 ohms. This means the output impedance is:
1 / ((1 / 316) + (1 / (9,684 + 100))) = 306 ohms
Thermal noise at 306 ohms is 3.15e-7 V. At -30 dB the output is 3.162% of the input. So voltage across R2 for a 2 V source is 0.06324 V. Thus the SNR is:
20 * log(3.15e-7 / 0.06324) = -106 dB
And if the music reaches a part 30 dB quieter, that’s -106 – 30 = -76 dB.
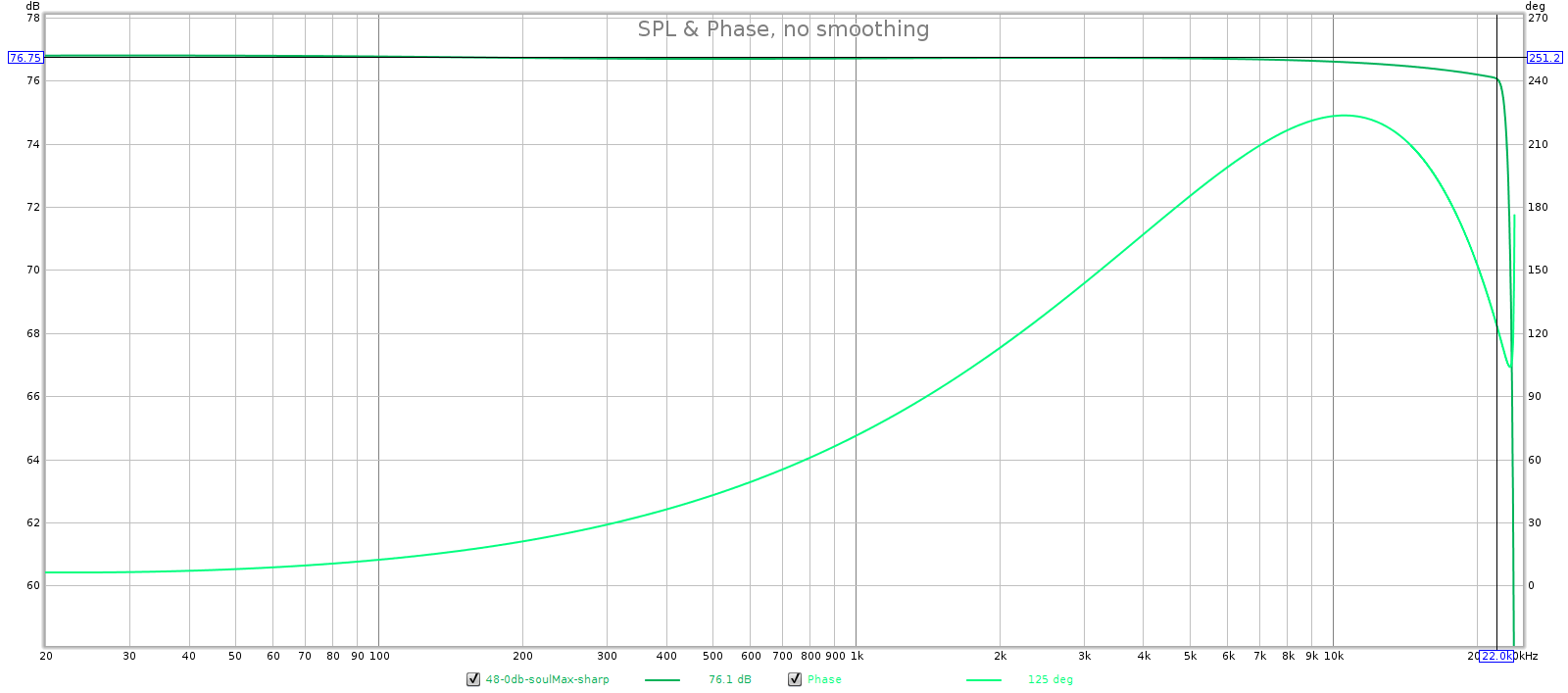
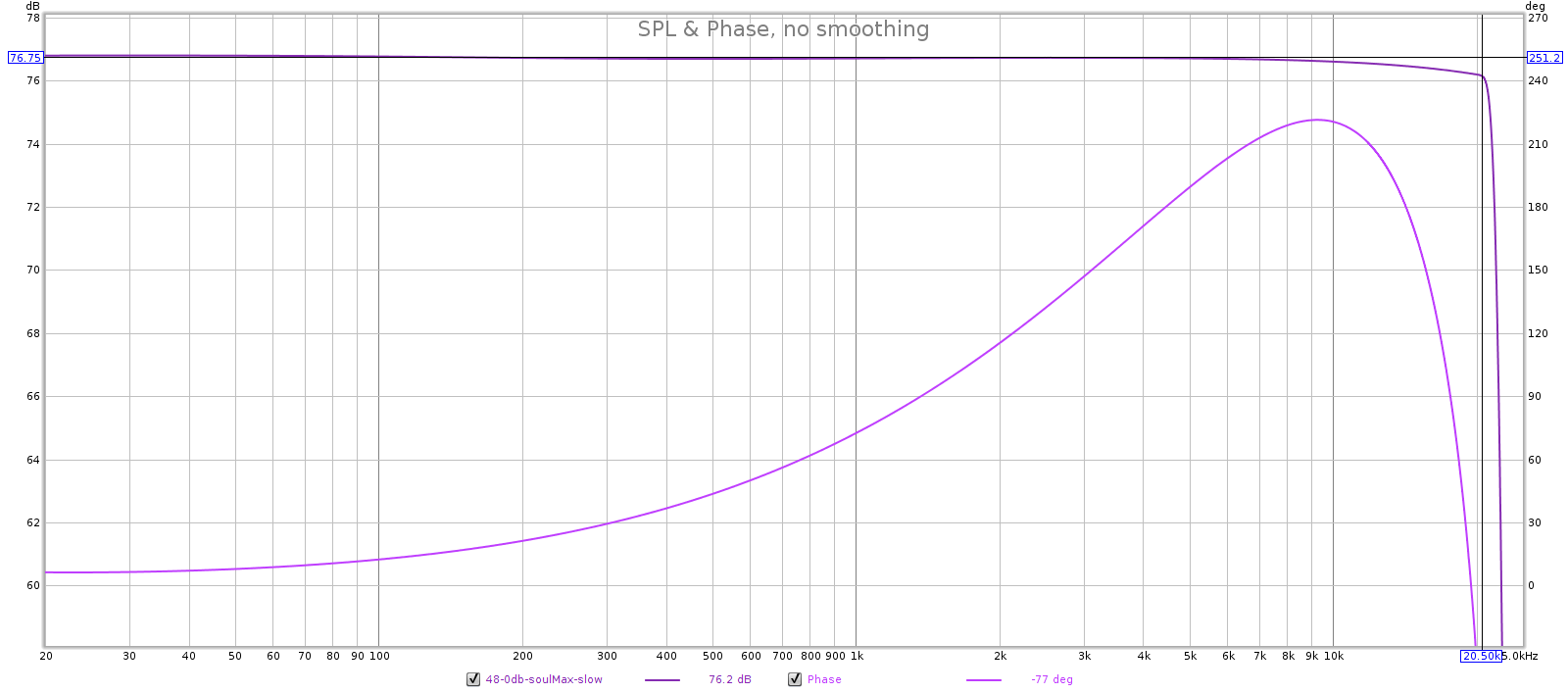
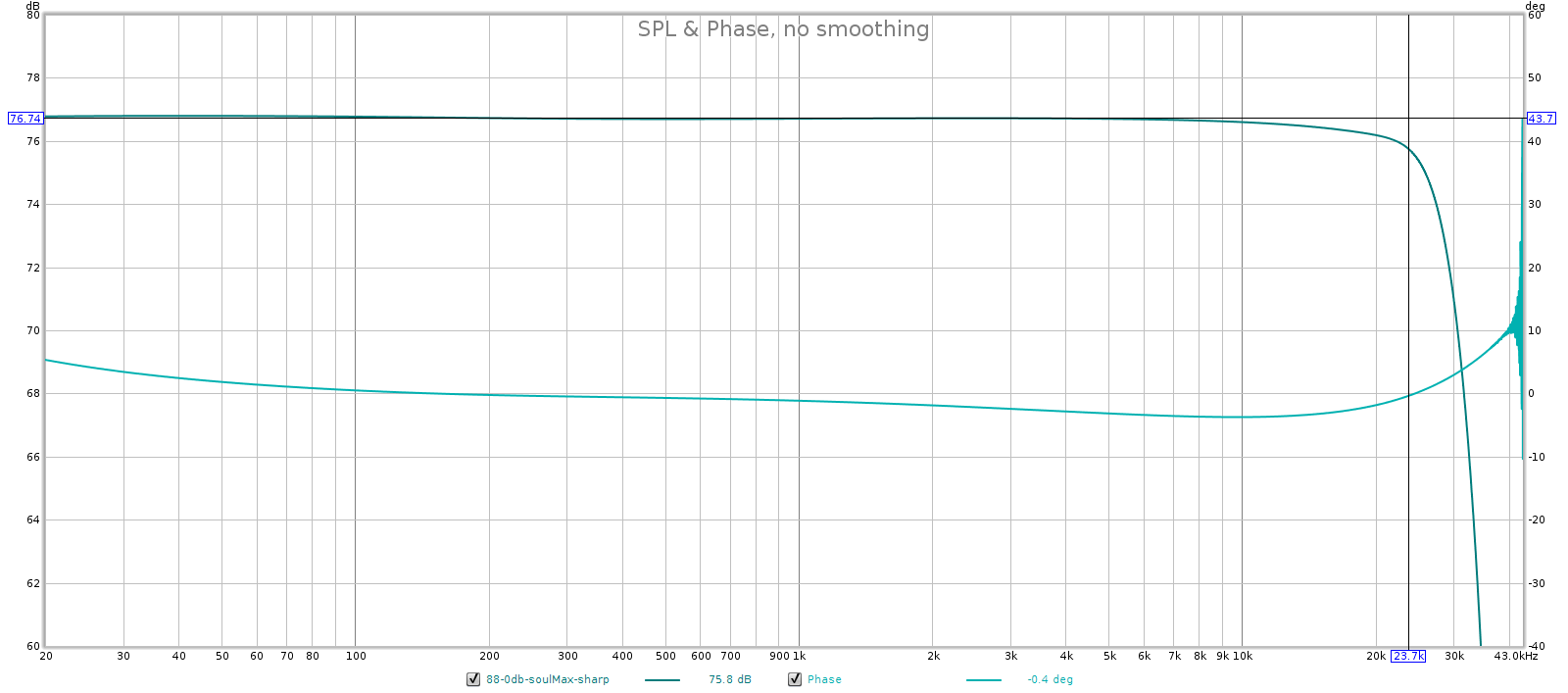
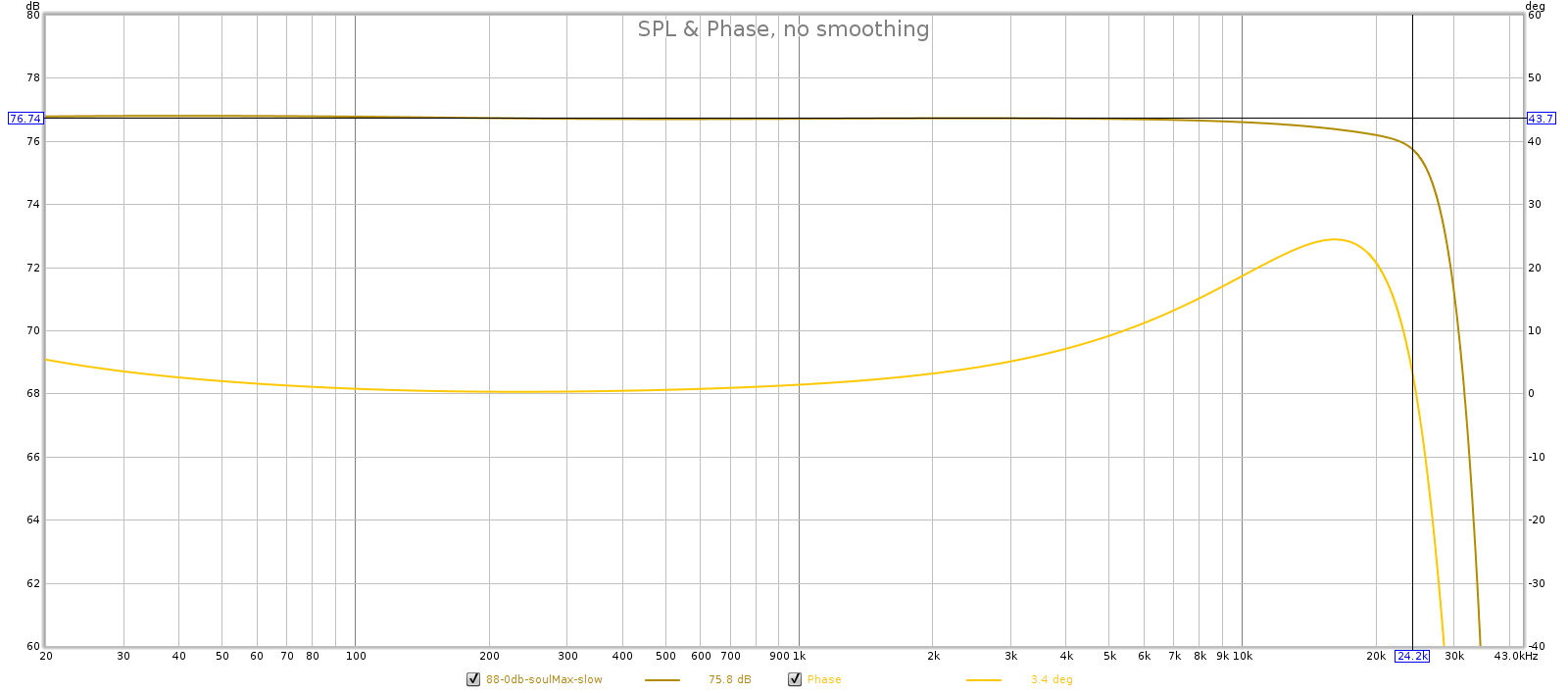
3.2 Frequency Response
Some people say passive attenuators have perfectly flat frequency response. Indeed, why wouldn’t they? They’re simple voltage dividers made of metal film resistors, and resistors have perfectly flat frequency frequency response! Alas, it’s not that simple.
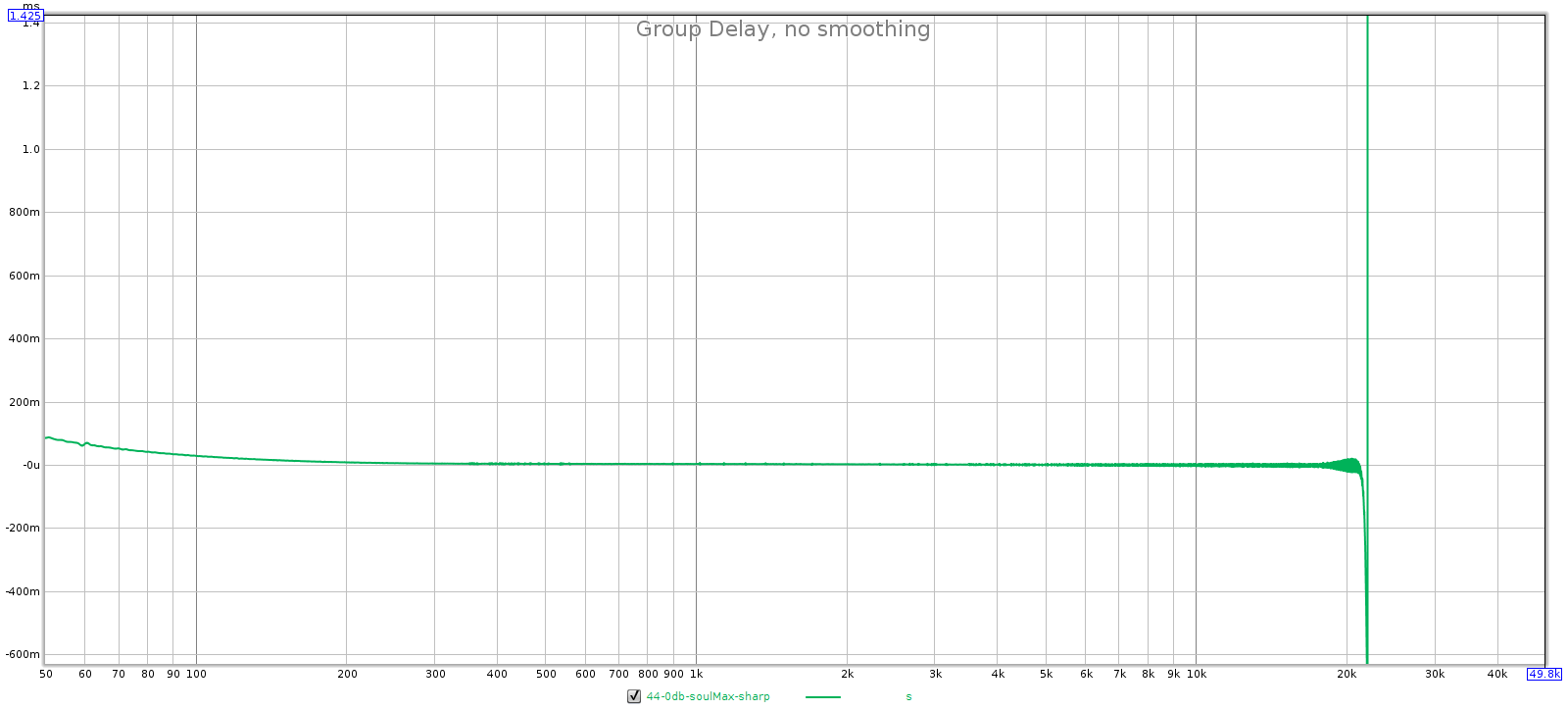
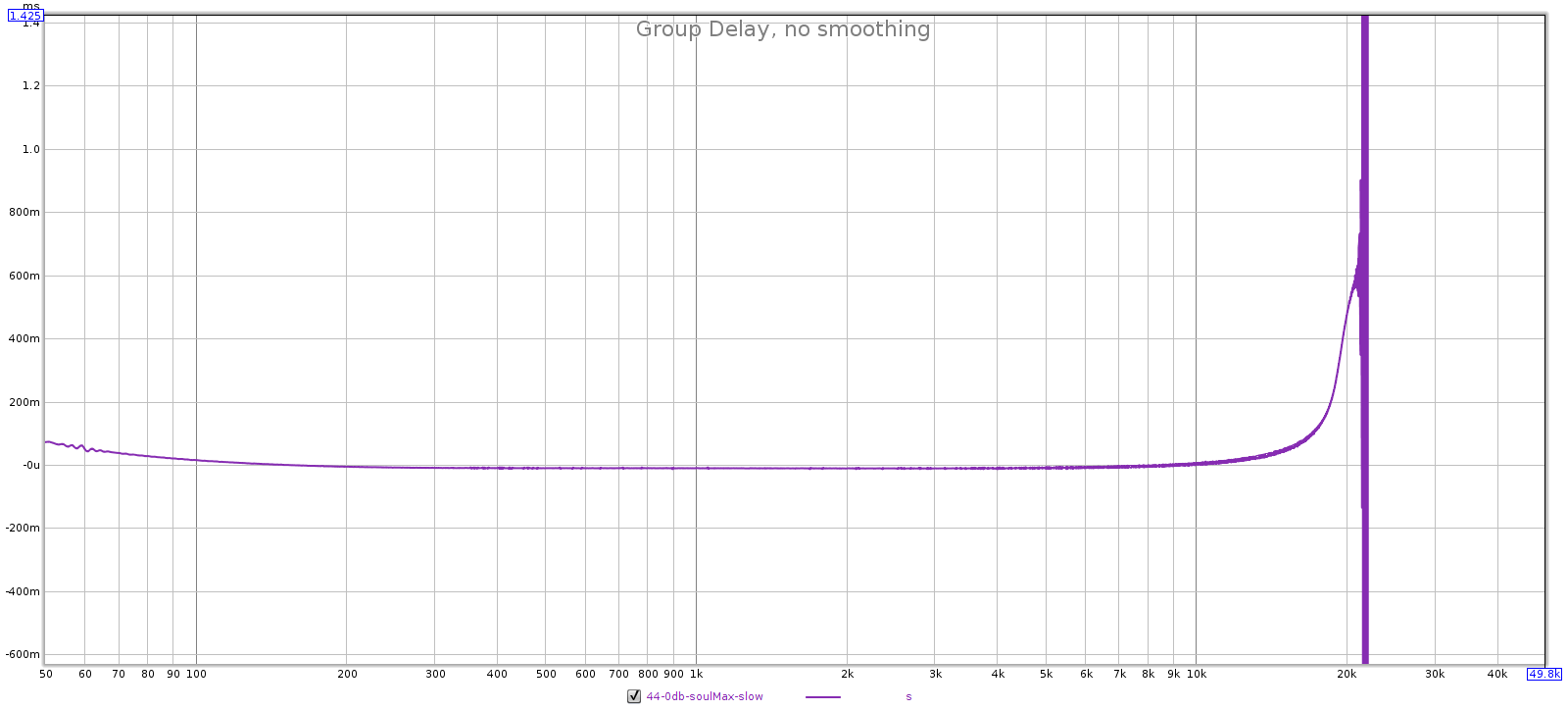
A passive attenuator is connected to a downstream device. The cables that connect it have some capacitance, and the attenuator’s output impedance combines with this capacitance to form an R-C circuit that acts as a low-pass filter. Put differently, the capacitance carries high frequencies to ground before they reach the downstream device. So the key question: what is the bandwidth of this filter?
Bandwidth is typically defined by the -3 dB point, which is the lowest frequency at which it attenuates by 3 dB. This has a simple equation:
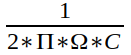
That is, it’s inversely proportional to the product of output impedance and cable capacitance. Because this defines the upper frequency response of the attenuator, we want this to be as big as possible. That means we want both output impedance and capacitance to be a small as possible.
So let’s plug in typical numbers. As explained above, the worst-case output impedance of our 10k attenuator is 2500 ohms (1250 ohms for a 5k attenuator). For cable, let’s take Blue Jeans LC-1, which is high quality yet inexpensive. Its capacitance is 12.2 pF per foot. That’s 12.2 pico-Farads, or trillions of a Farad = 12.2 * 10^-12 Farads. With 6 feet of this cable between the passive preamp and downstream device, we have 12.2 * 6 = 73.2 pF of capacitance.
The above formula gives us 870,000, or 870 kHz. That’s the frequency at which this passive attenuator is down 3 dB. And that is the worst-case! For example at -30 dB attenuation, the output impedance is 306 ohms so the bandwidth is 7.1 MHz.
In short, the passive attenuator has perfectly flat frequency response in the audible spectrum. It’s true that a passive attenuator can attenuate frequencies in the audible spectrum, but this concern is more theoretical than practical. That would take ridiculously high capacitance (poorly engineered) cables or long runs. In our example, to bring the -3 dB point down to 20 kHz you can compute it would require about 260 feet of cable!
4. Comparison to Active Preamps
Most active preamps have a fixed gain stage with attenuation. Usually the attenuation is upstream from the gain, because that helps prevent input voltage clipping. But it has the drawback that any noise added by the attenuation potentiometer is amplified by the gain ratio. Furthermore, the amount of noise, which depends largely on the gain ratio, is constant regardless of the signal level. This means as you turn down the volume, the SNR drops with it.
The SNR of amps and preamps is measured at full output. But this is misleading, since nobody actually listens at full output. When was the last time you listened to music with the volume set to full blast? With typical listening levels 20 to 40 dB below full output, the SNR you actually hear when listening is 20 to 40 dB less than advertised.
You can see this in practice on many of the reviews at Audio Science Review. The SNR at 50 mV output is typically 30-40 dB lower than the SNR at full volume. With full volume normally being 2 V, that’s 32 dB of attenuation giving 30-40 dB worse SNR.
Consider an ultra-high quality active preamp having an SNR of 120 dB at full scale 2.0 V output. When you turn it down to a typical listening level, say -30 dB, the SNR drops to the mid 80s. If you took the full scale output of that preamp and sent it to a passive attenuator having the same 30 dB of attenuation, the SNR would be 106 dB. The passive attenuator is 20 dB quieter than the active preamp.
In summary, at full volume a passive attenuator has no advantage. But at the lower levels that we actually listen, they have:
- Lower noise.
- Lower distortion.
- Perfectly flat frequency response at audio frequencies.
Of course, this assumes the system meets the requirements listed earlier (most systems do).
4.1 Exceptions
Here are the exceptions that prove the rule. Some active preamps are designed for improved performance (lower noise) at low volume settings.
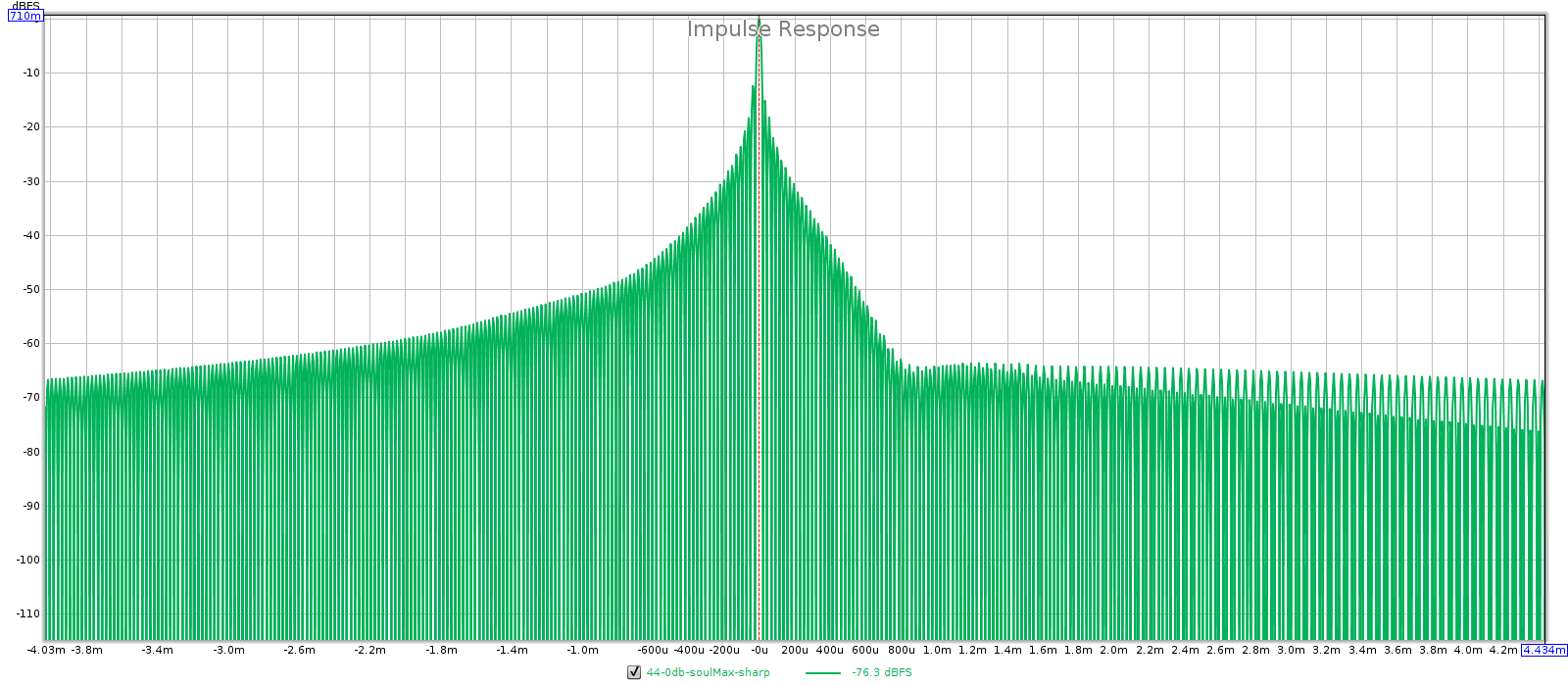
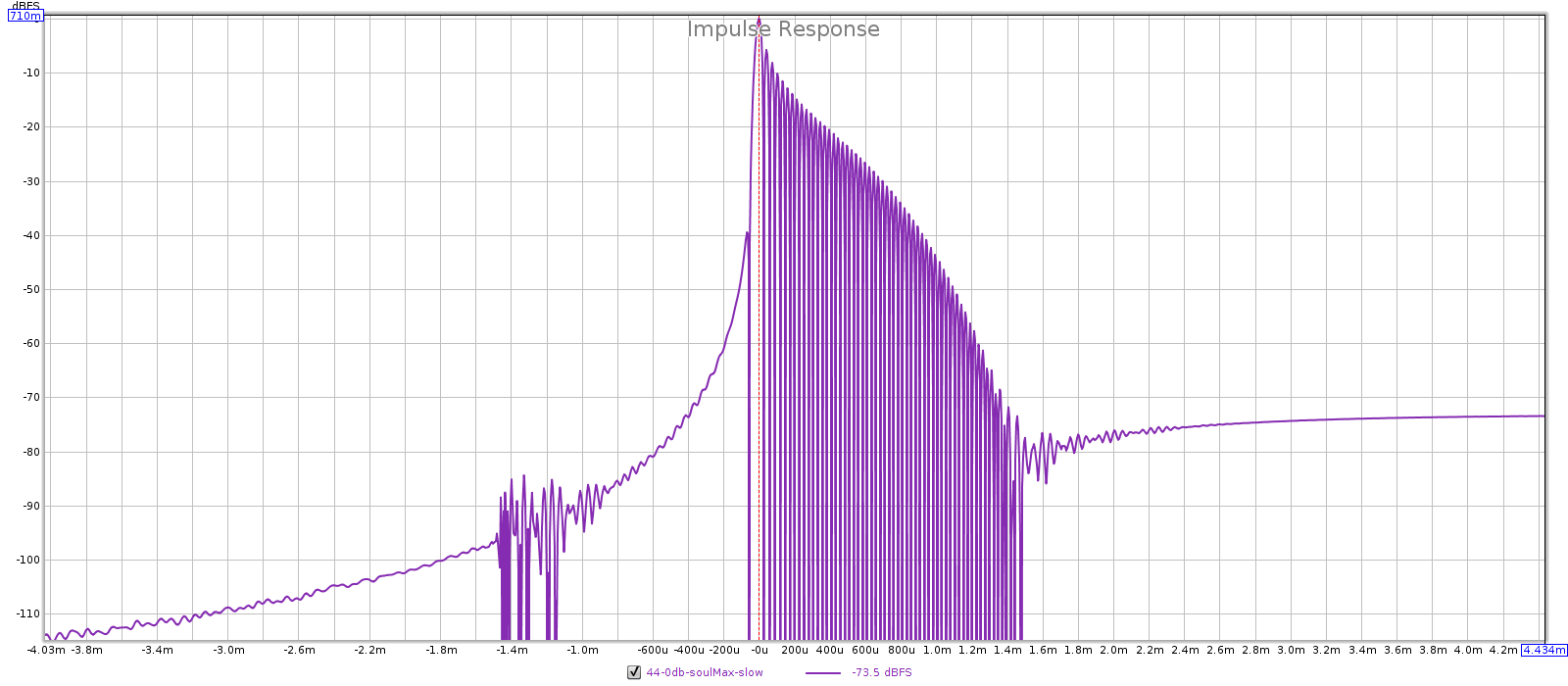
One way is to put the volume potentiometer downstream from the gain stage. This has 2 advantages: first, pot noise is not amplified by the gain ratio. Second, it attenuates the signal after the gain noise has been added, so it attenuates both the signal and the noise. The drawback is that this exposes the gain stage directly to the source voltages, so it will clip if those voltages are too high. The JDS Atom is an example of this design and it has great low volume performance. At 2 V its SNR is 120 dB, and at 50 mV it is 92 dB. As you turn the volume down by -32 dB, the SNR drops by 28 dB. This is less than 1:1, where most preamps are more than 1:1.
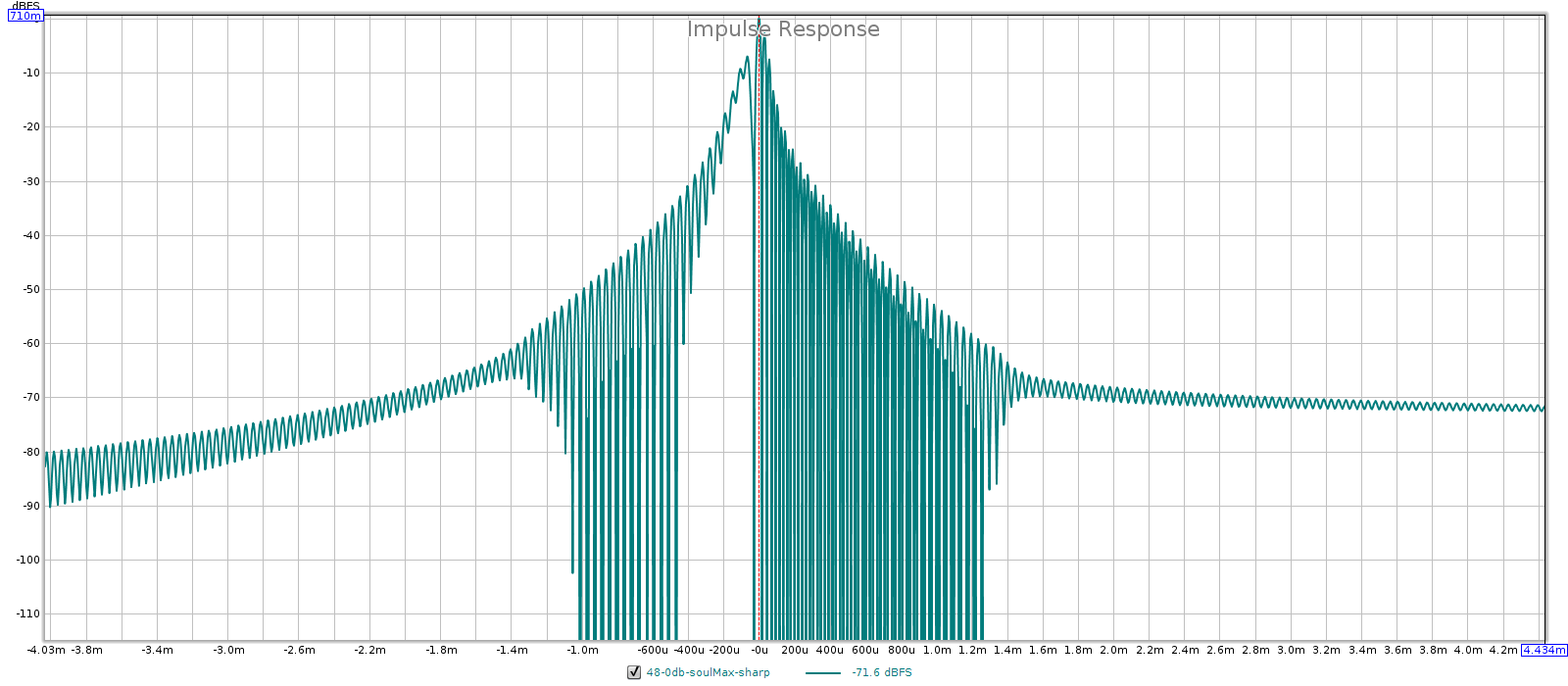
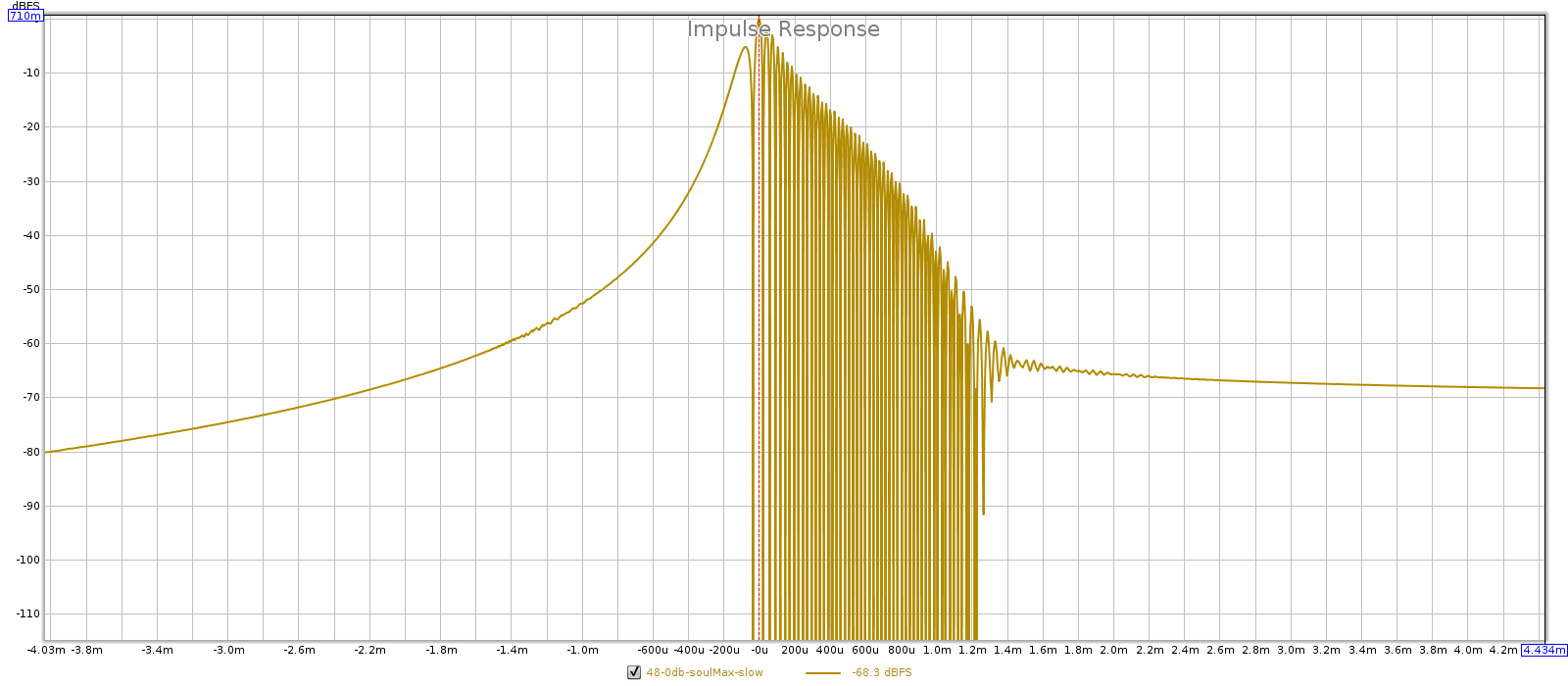
Another way is for the preamp to change its gain ratio, instead of using a fixed gain ratio with attenuation. As you turn down the volume, you reduce the gain ratio, which reduces noise & distortion (and widens bandwidth). This requires less than unity gain, which can be done with an inverting gain-feedback loop. Of course, this entirely obviates the need for separate attenuation. The volume control changes the “R1” and “R2” metal film resistors in the gain-feedback loop. This is an unusual design that some Meier Audio amps use, and they have the lowest noise I’ve measured — the Corda Soul measures even lower noise than the JDS Atom.
In summary, at the low to medium volumes we actually use for listening, a passive attenuator has better SNR than conventional active designs. But there are a few actives of unusual design that can equal or exceed the performance of a passive.